© 2020 - 2023 Mr. Eric

Euclid Book I PROP. XXXI. -- PROBLEM.
Through a given point (C) to draw a right line parallel to a given right line.

Euclid Book I PROP. XXX. -- THEOREM.
If two right lines (AB, CD) be parallel to the same right line (EF), they are parallel to one another.
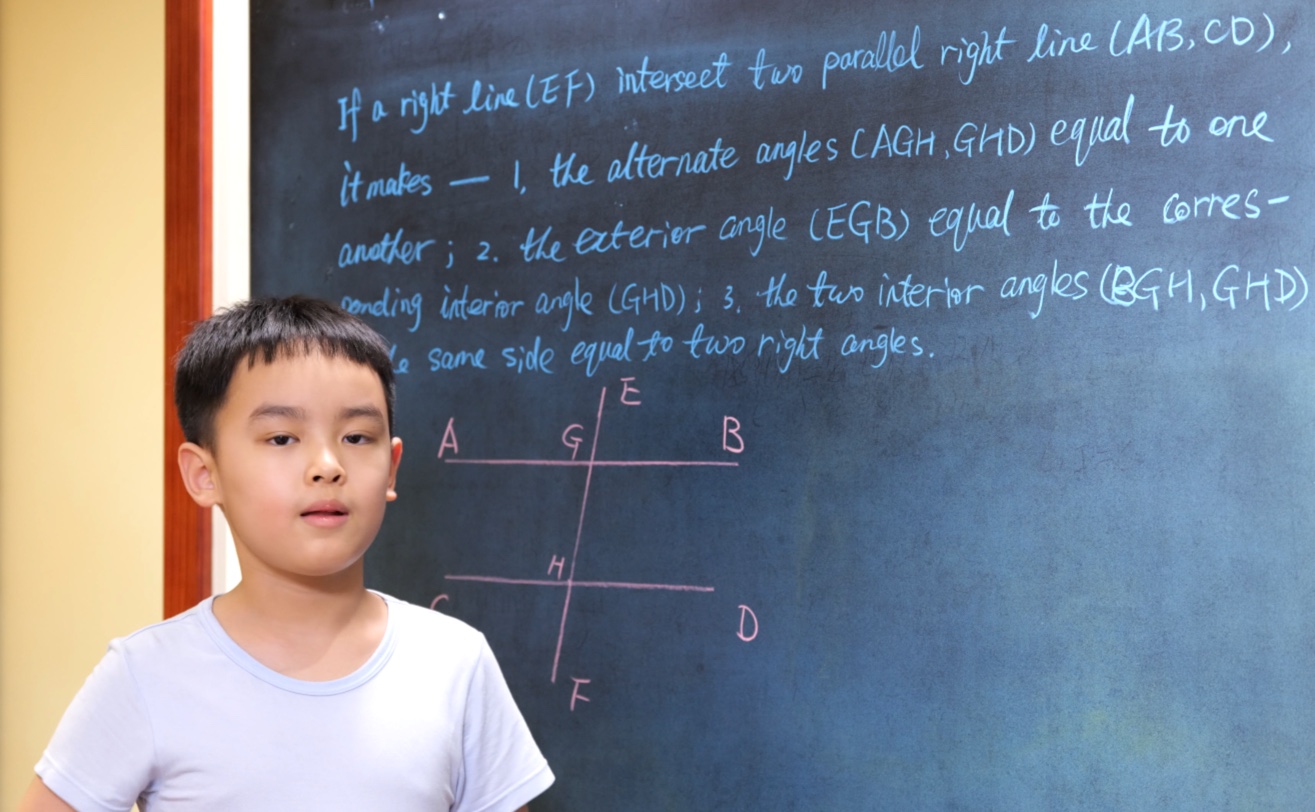
Euclid Book I PROP. XXIX. -- THEOREM.
If a right line (EF) intersect two parallel right lines (AB, CD), it makes:
- the alternate angles (AGH, GHD) equal to one another;
- the exterior angle (EGB) equal to the corresponding interior angle (GHD);
- the two interior angles (BGH, GHD) on the same side equal to two right angles.

Euclid Book I PROP. XXVIII. -- THEOREM.
If a right line (EF) intersect two parallel right lines (AB, CD) makes the exterior angle (EGB) equal to its corresponding interior angle (GHD), or makes two interior angles (BGH, GHD) on the same side equal to two right angles, the two right lines are parallel.
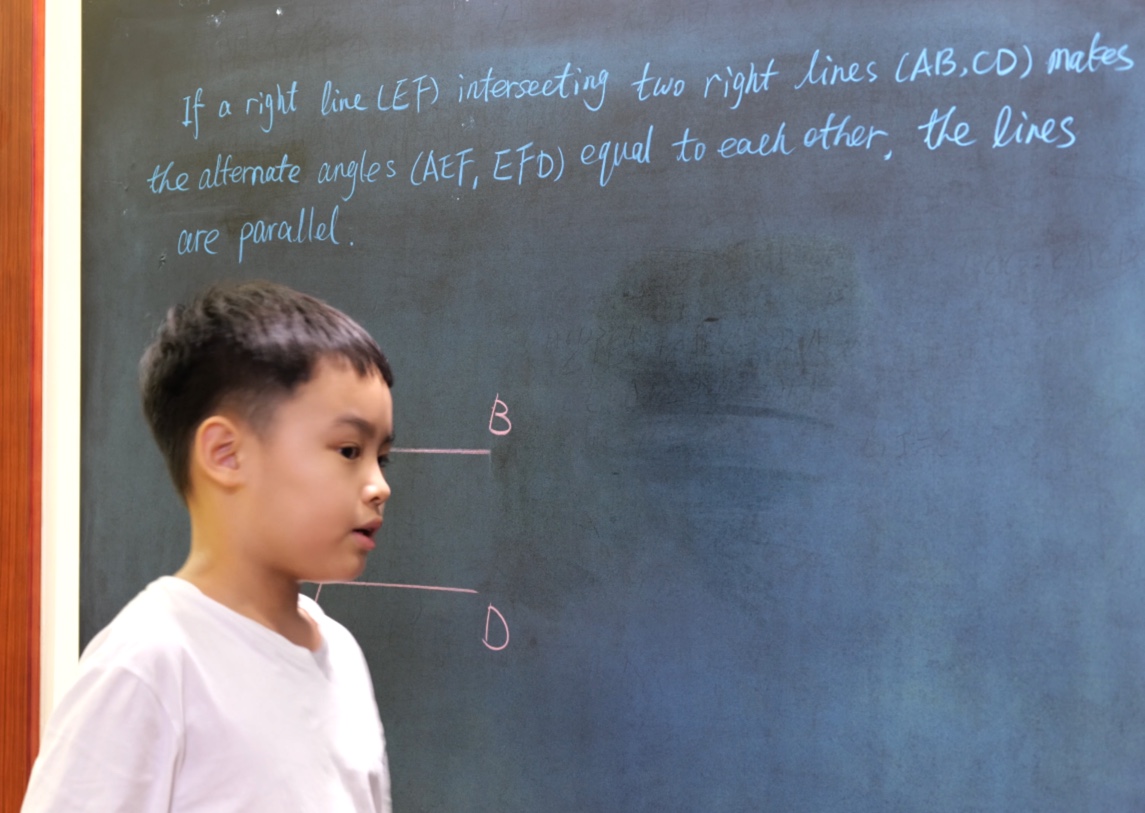
Euclid Book I PROP. XXVII. -- THEOREM.
If a right line (EF) intersecting two right lines (AB, CD) makes the alternate angles (AEF, EFD) equal to each other, these lines are parallel.

Euclid Book I PROP. XXVI. -- THEOREM.
If two triangles (ABC, DEF) have two angles B, C) of one equal respectively to two angles (E, F) of the other, and a side of one equal to a side similarly placed with respect to the equal angles of the other, the triangles are equal in every respect.

Euclid Book I PROP. XXV. -- THEOREM.
If two triangles (ABC, DEF) have two sides (AB, AC) of one respectively equal to two sides (DE, DF) of the other, but the base (BC) of one greater than the base (EF) of the other, the angle (A) contained by the sides of that which has the greater base is greater them the angle (D) contained by the sides of the other.
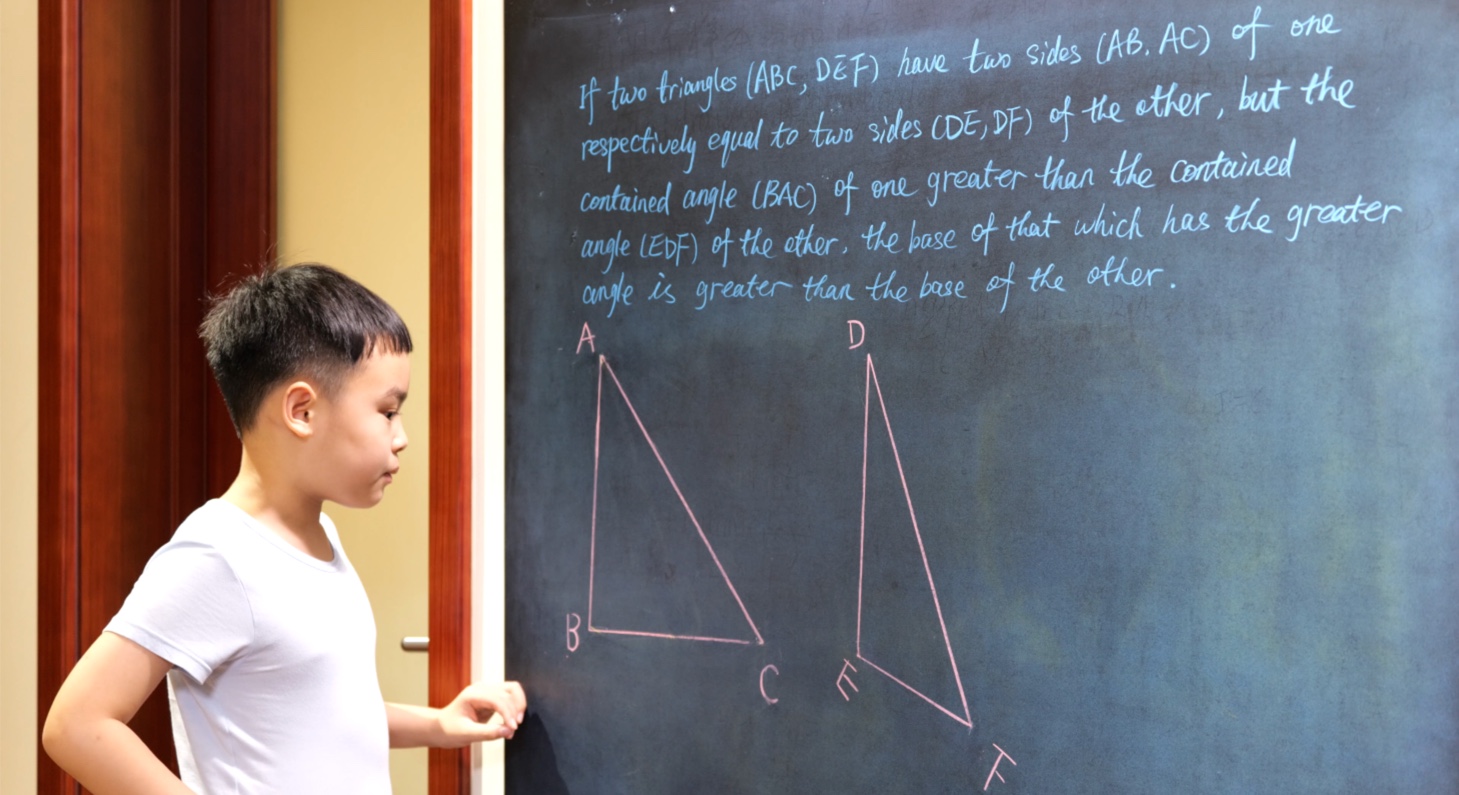
Euclid Book I PROP. XXIV. -- THEOREM.
If two triangles (ABC, DEF) have two sides (AB, AC) of one respectively equal to two sides (DE, DF) of the other, but the contained angle (BAC) of one greater than the contained angle (EDF) of the other, the base of that which has the greater angle is greater than the base of the other.

Euclid Book I PROP. XXIII. -- PROBLEM.
At a given point (A) in a given right line (AB) to make an angle equal to a given rectilineal angle (DEF)
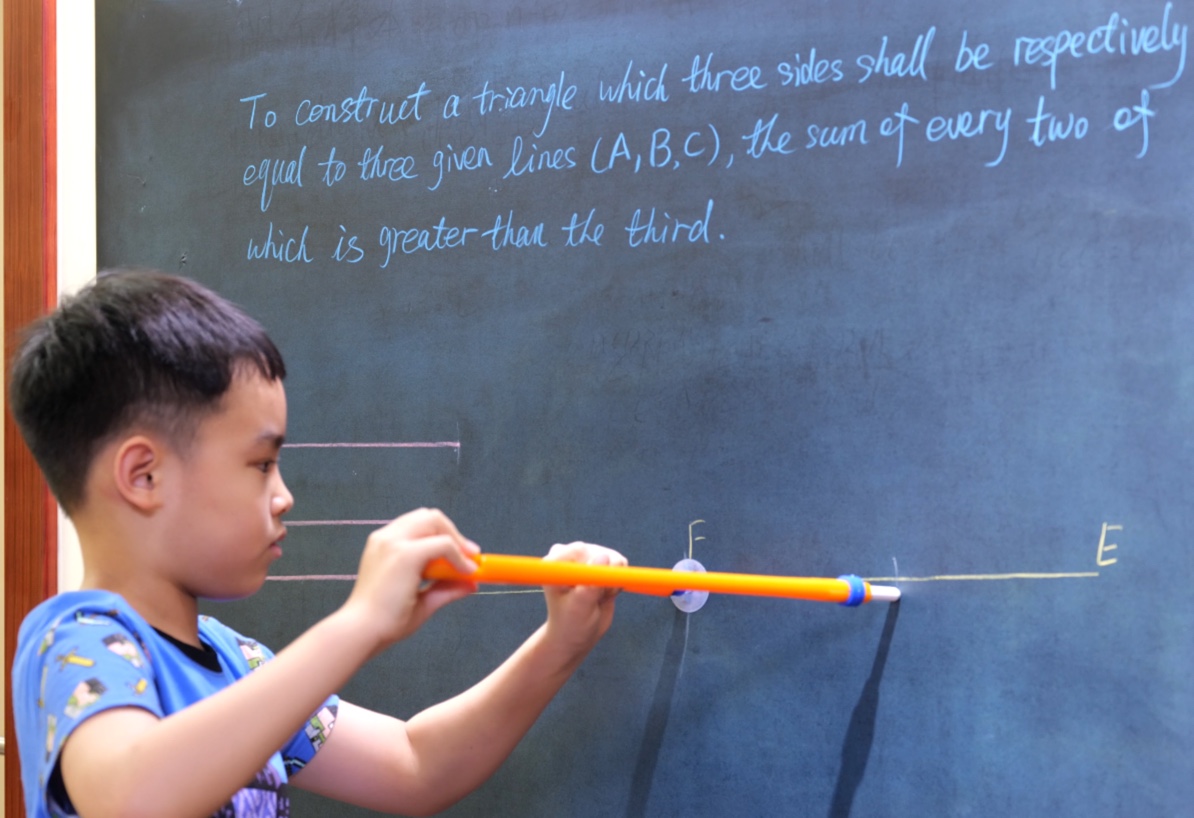
Euclid Book I PROP. XXII. -- PROBLEM.
To construct a triangle which three sides shall be respectively equal to three given lines (A, B, C), the sum of every two of which is greater than the third.
Mr. Eric
I am a student, learn, happy.
Always happy.