Mr. Eric

Life writes the best stories. Let’s study together! Never copy please!

Have you ever volunteered before? If you haven’t, then you should try your best to volunteer more. However, you don’t need to volunteer because everyone has their civil rights, which don’t force you to volunteer. Therefore you could not do it if you can’t, or don’t want to do it!

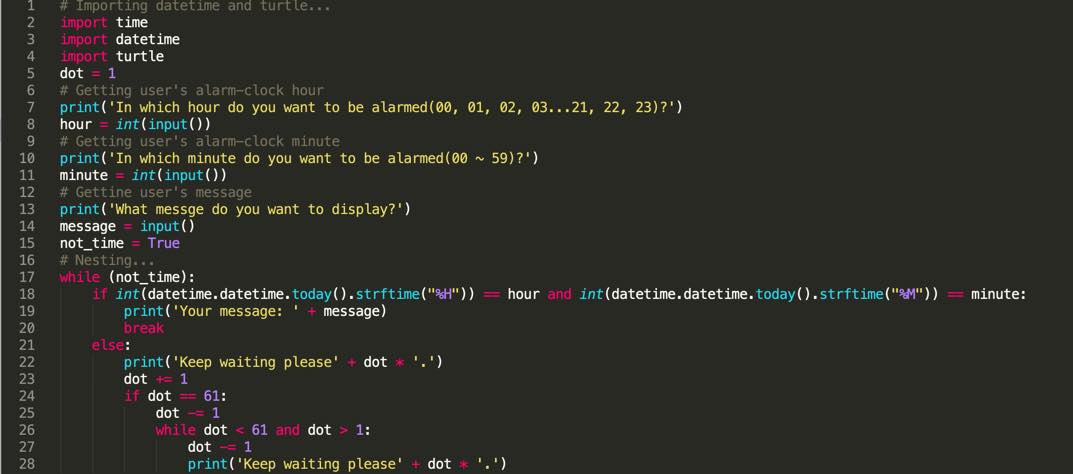
Many personal computers, laptop computers, tablets, and smart phones have applications that allow a user to set reminder alarms. To accomplish this, all these applications use date and time functions that are built into the language they are programmed in.

Had you ever met a homeless person? Did you decide to help them of not? However, it’s important to help them anyway you could, normal people should, and could help the homeless. but if he don’t needs help, you could leave him alone for some time. There might be someone which could help him! Here’s a story:

In any triangle (ABC), the square on any side subtending an acute angle (C) is less than the sum of the squares on the sides containing that angle, by twice the rectangle (BC, CD) contained by either of them (BC) and the intercept (CD) between the acute angle and the foot of the perpendicular on it from the opposite angle.

a. Assume that the length and width of a rectangle can be only whole numbers. How many rectangles of different dimensions have a perimeter of 12? 14? 16? 18? 24? (Orientation of the rectangle does not matter; that is, a 2x3 is the same rectangle as a 3x2.)

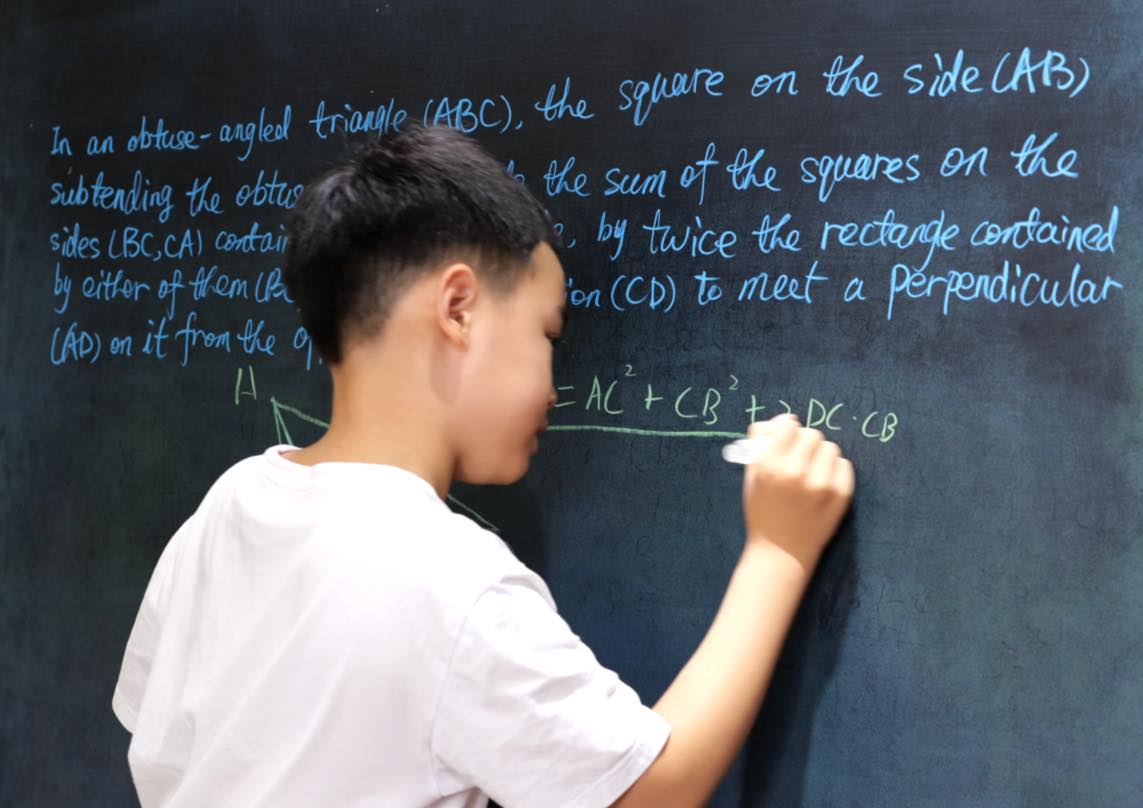
In an obtuse-angled triangle (ABC), the square on the side (AB) subtending the obtuse angle exceeds the sum of squares on the sides (BC, CA) containing the obtuse angle, by twice the rectangle contained by either of them (BC), and its continuation (CD) to meet a perpendicular (AD) on it from the opposite angle.

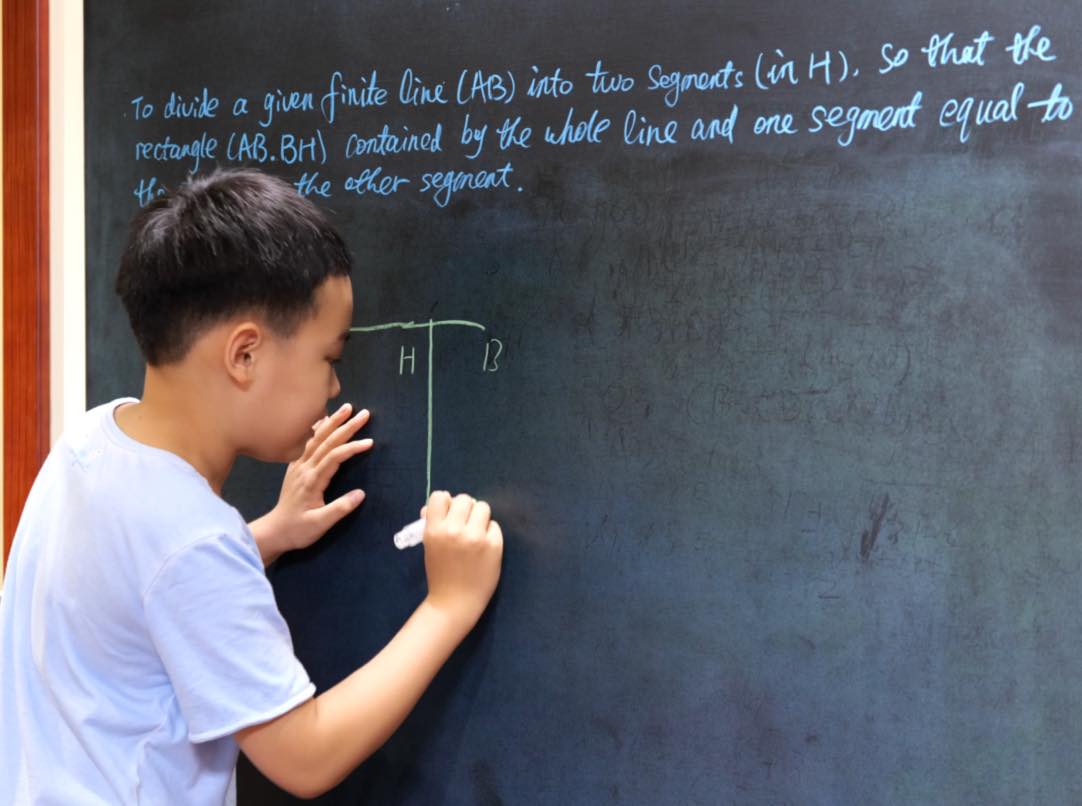
To divide a given finite line (AB) into two segments (in H), so that the rectangle (AB. BH) contained by the whole line and one segment may be equal to the square on the other segment.

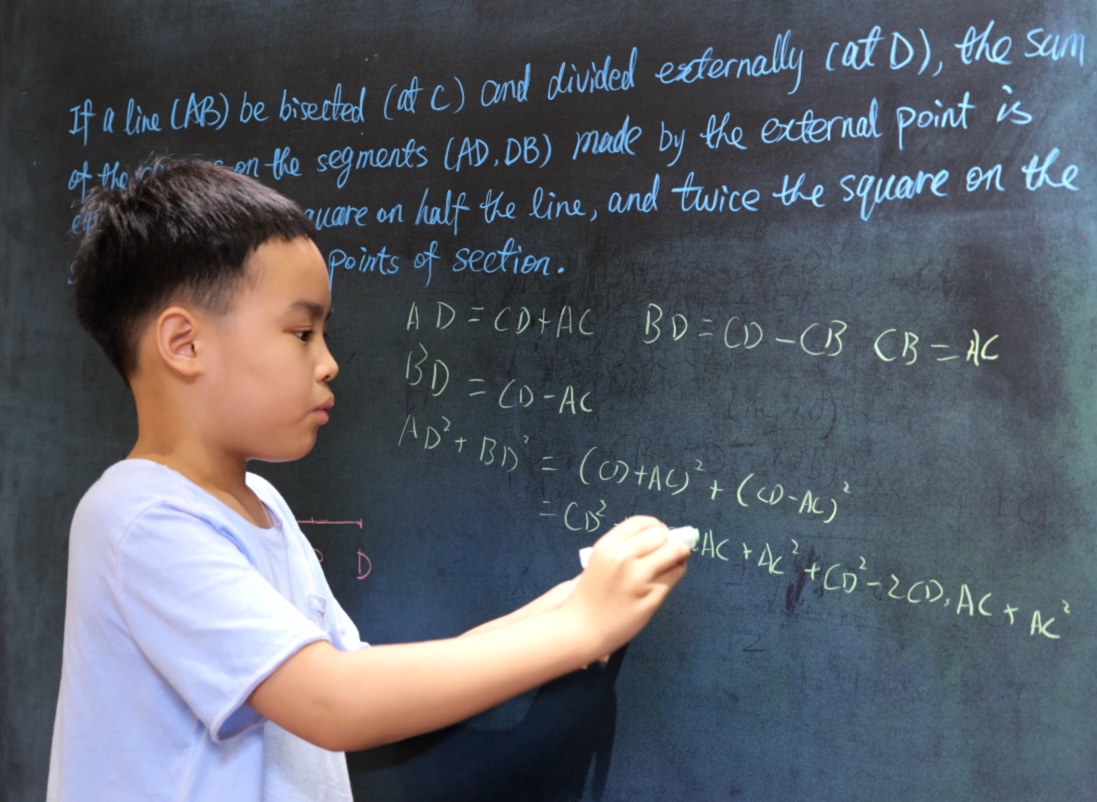
If a line (AB) be bisected (at C) and divided externally (at D), the sum of the squares on the segments (AD, DB) made by the external point is equal to twice the square on half the line, and twice the square on the segment between the points of section.

If a line (AB) be bisected (at C) and divided into two unequal parts (at D), the sum of the squares on the unequal parts (AD, DB) is double the sum of the squares on half the line (AC), and on the segment (CD) between the points of section.

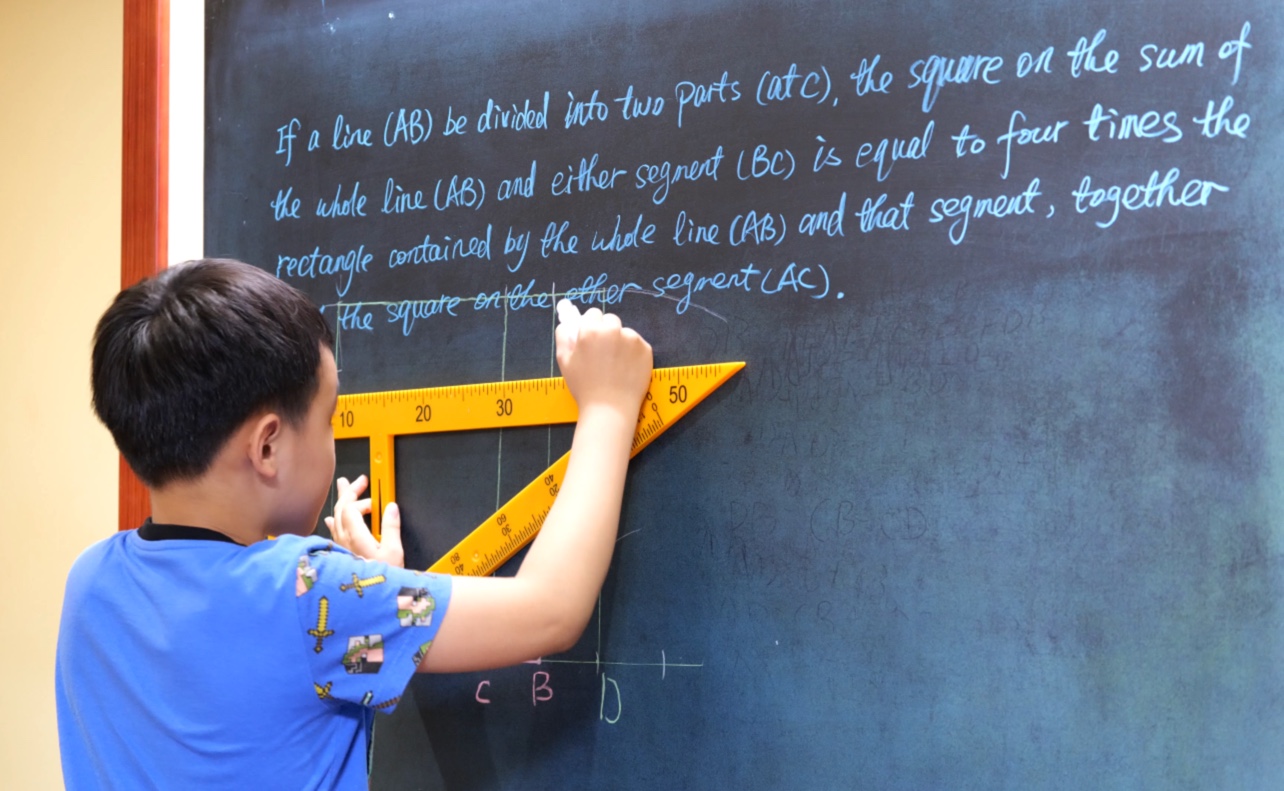
If a line (AB) be divided into two parts (at C), the square on the sum the whole line (AB) and either segment (BC) is equal to four times the rectangle contained by the whole line (AB) and that segment, together with the square on the other segment (AC).