Mr. Eric
Life writes the best stories. Let’s study together! Never copy please!
© 2020 - 2023 Mr. Eric
© 2020 - 2023 Mr. Eric
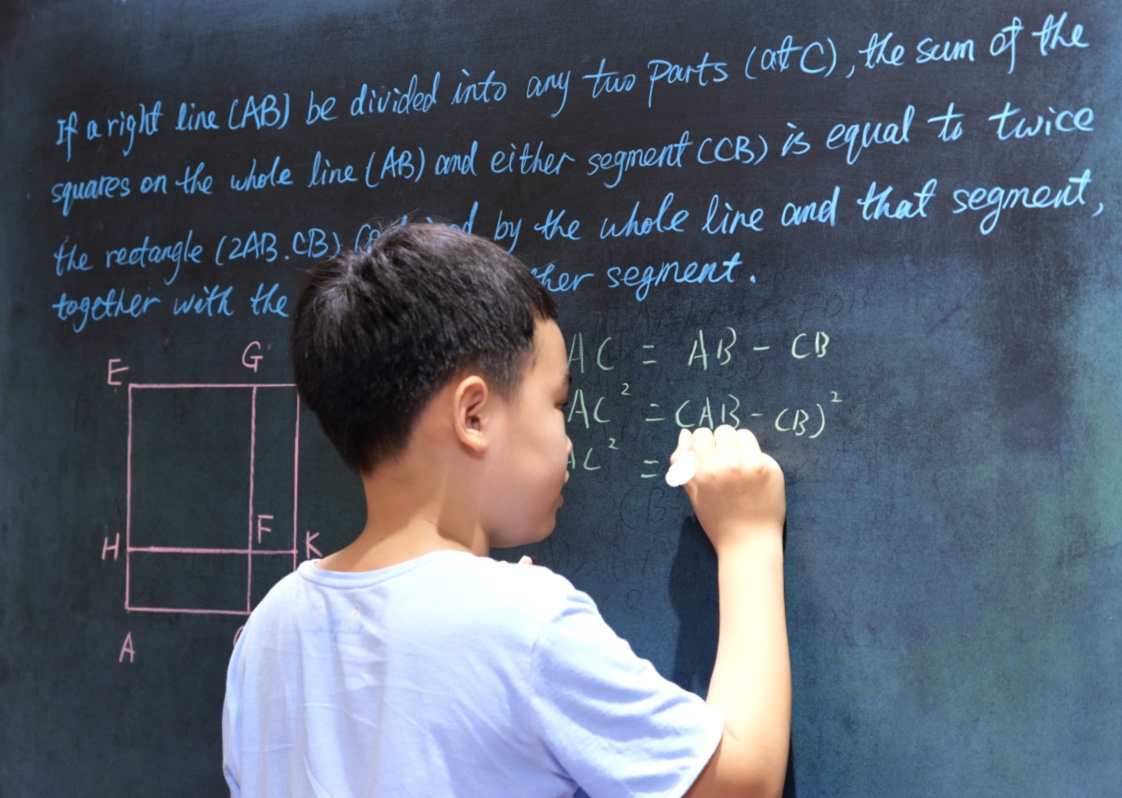
If a right line (AB) be divided into any two parts (at C), the sum of the squares on the whole line (AB) and either segment (CB) is equal to twice the rectangle (2AB.CB) contained by the whole line and that segment, together with the square on the other segment.

If a line (AB) be bisected (at C), and divided externally in any point (D), the rectangle (AD.BD) contained by the segments made by the external point, together with the square on half the line, is equal to the square on the segment between the middle point and the point of external division.
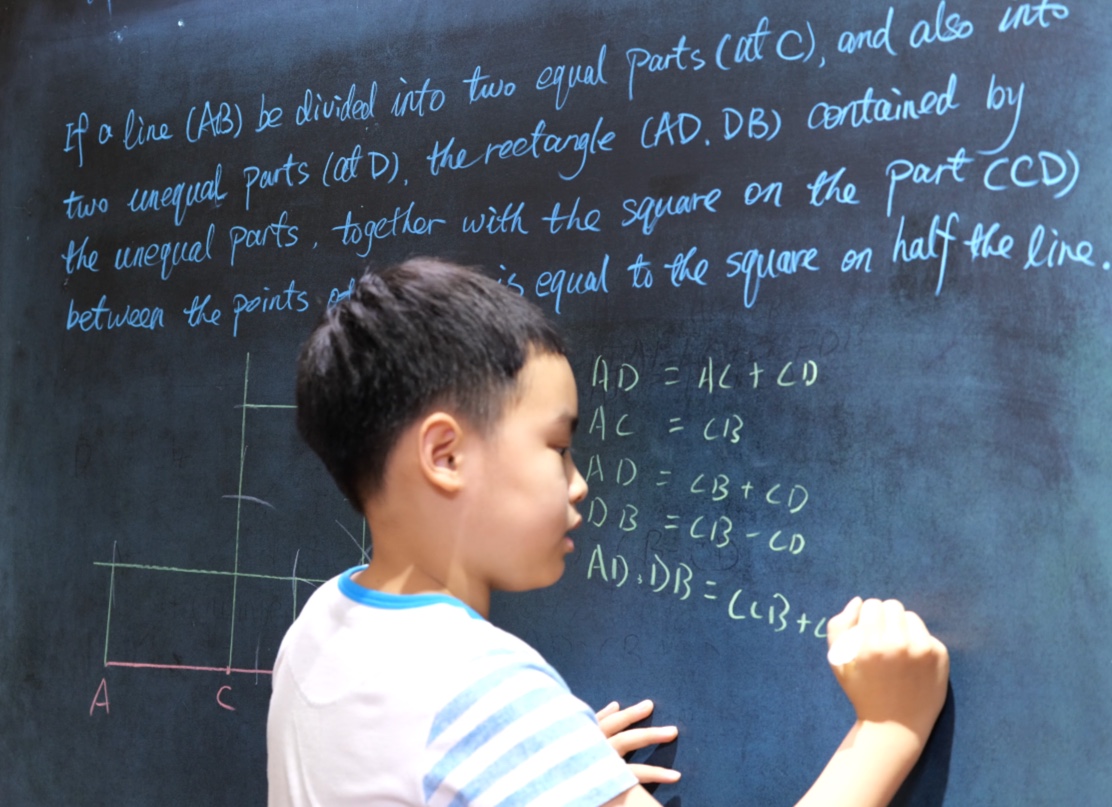
If a line (AB) be divided into two equal parts (at C), and also into two unequal parts (at D), the rectangle (AD.DB) contained by the unequal parts, together with the square on the part (CD) between the points of section, is equal to the square on half the line.

If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the squares on the parts (AC, CB), together with twice their rectangle.
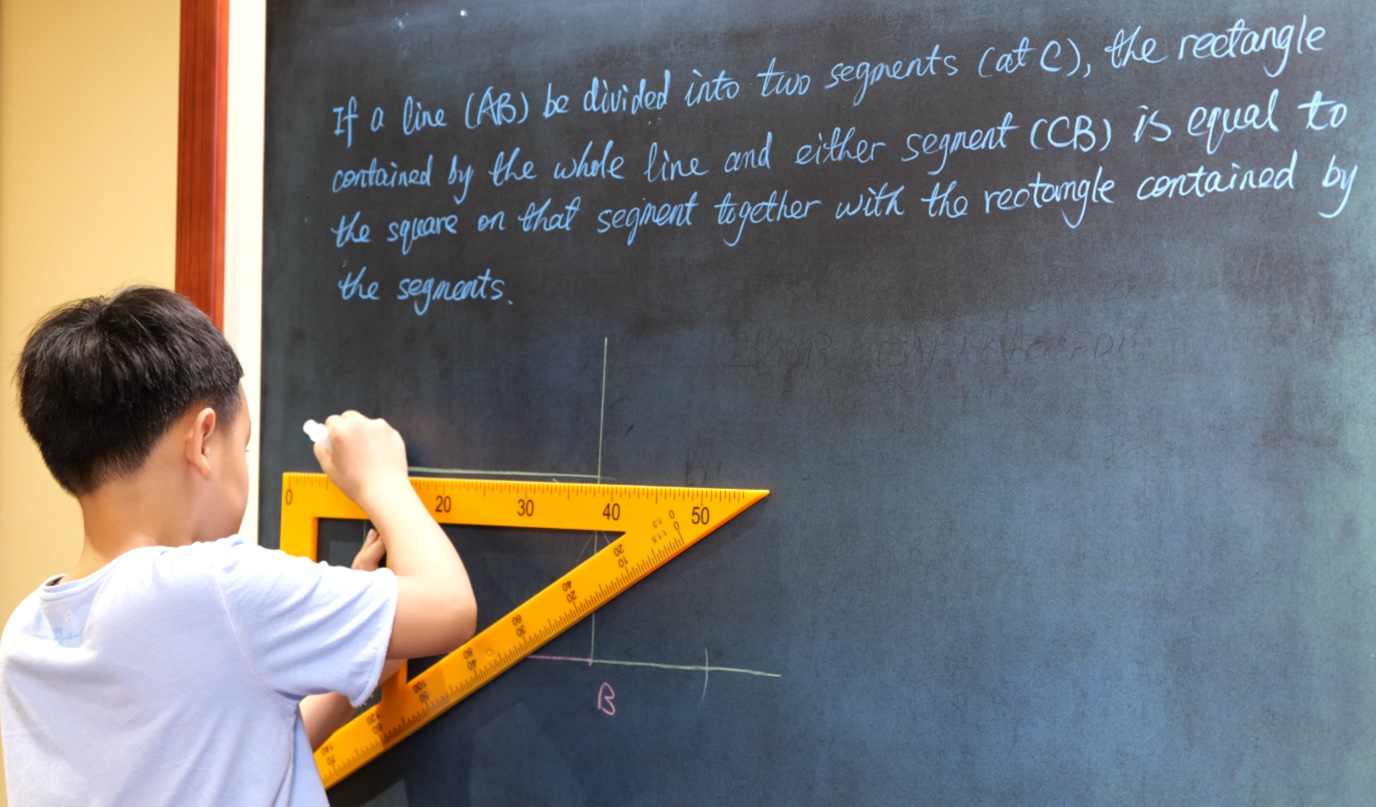
If a line (AB) be divided into two segments (at C), the rectangle contained by the whole line and either segment (CB) is equal to the square on that segment together with the rectangle contained by the segments.
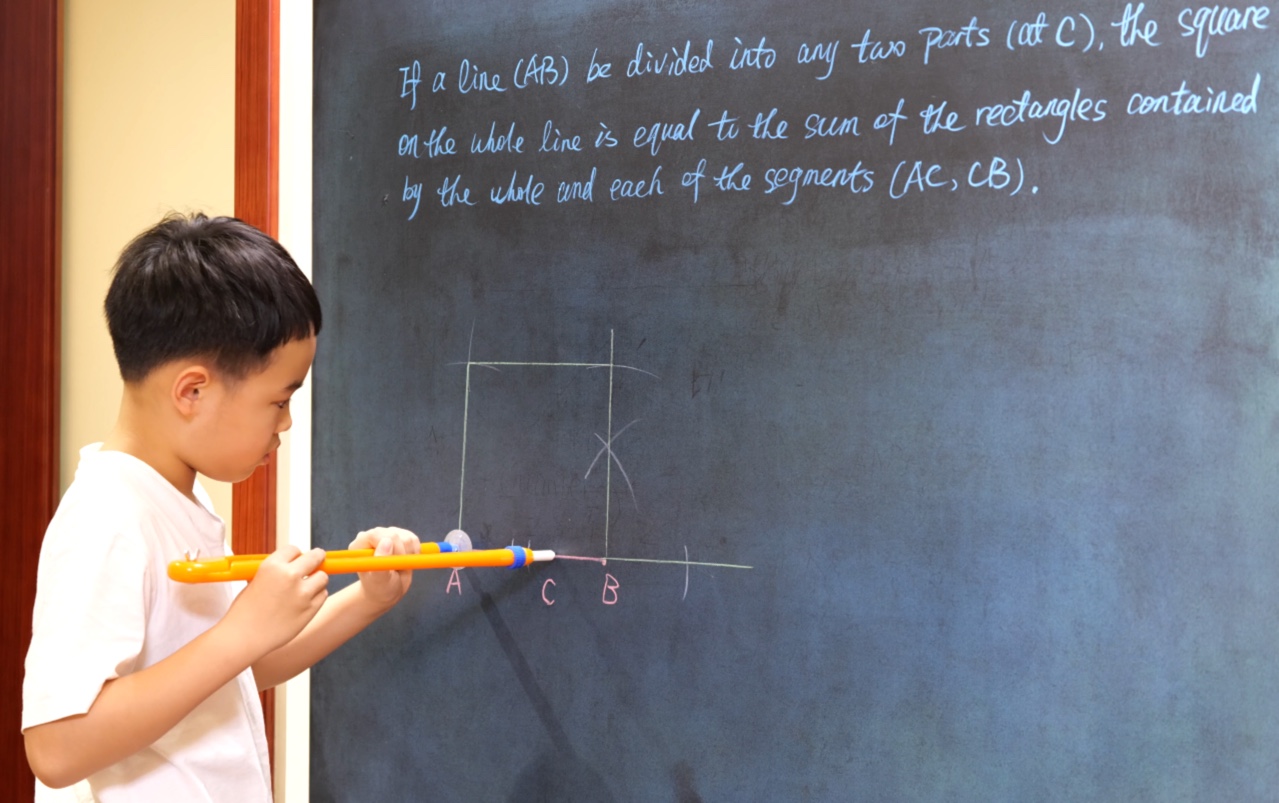
If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the rectangles contained by the whole and each of the segments (AC, CB).
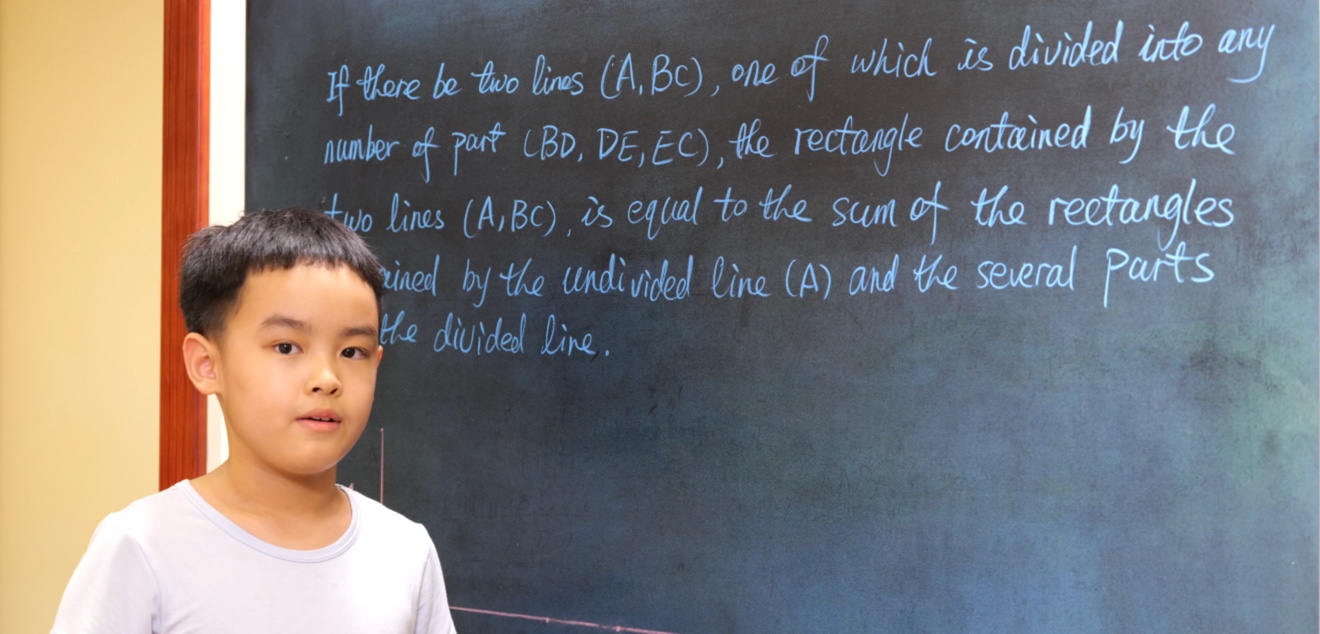
If there be two lines (A, BC), one of which is divided into any number of parts (BD, DE, EC), the rectangle contained by the two lines (A, BC), is equal to the sum of the rectangles contained by the undivided line (A) and the several parts of the divided line.
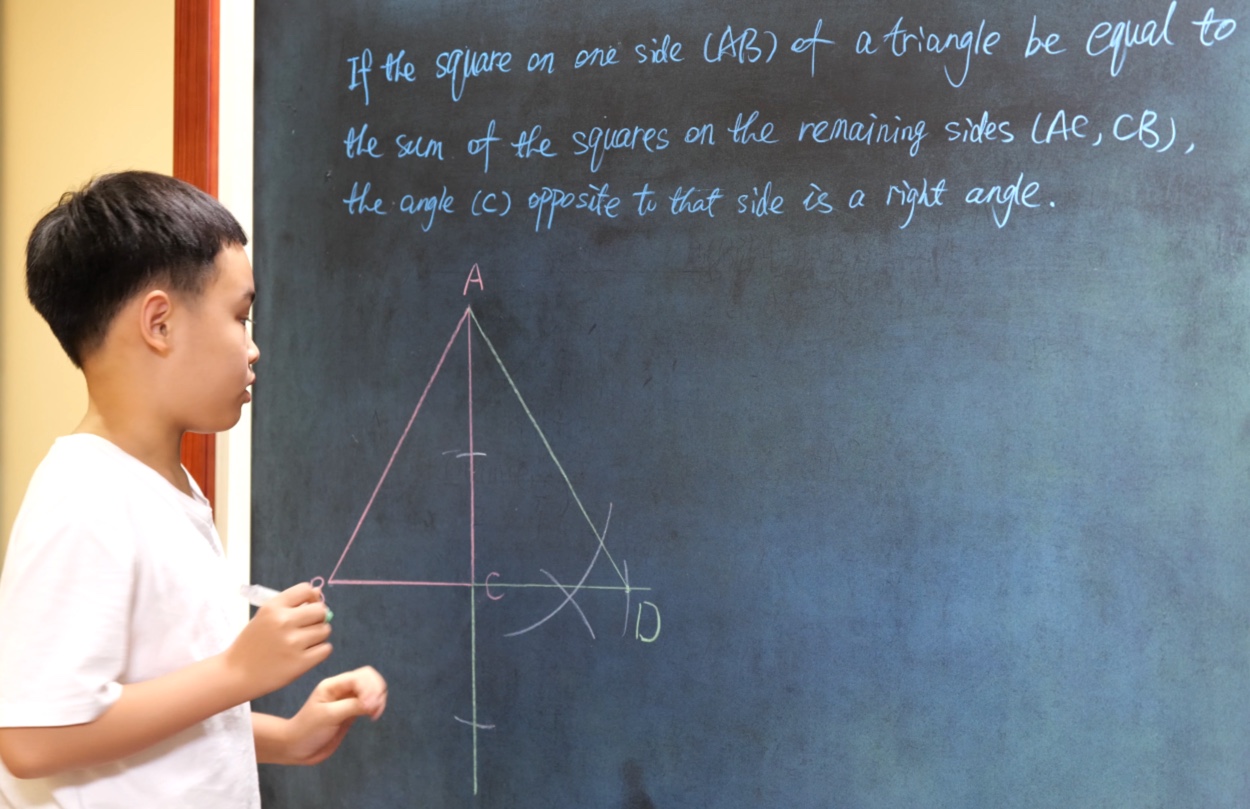
If the square on one side (AB) of a triangle be equal to the sum of the squares on the remaining sides (AC, CB), the angle (C) opposite to that side is a right angle.

In a right-angled triangle (ABC) the square on the hypotenuse (AB) is equal to the sum of the squares on the other two sides (AC, BC).
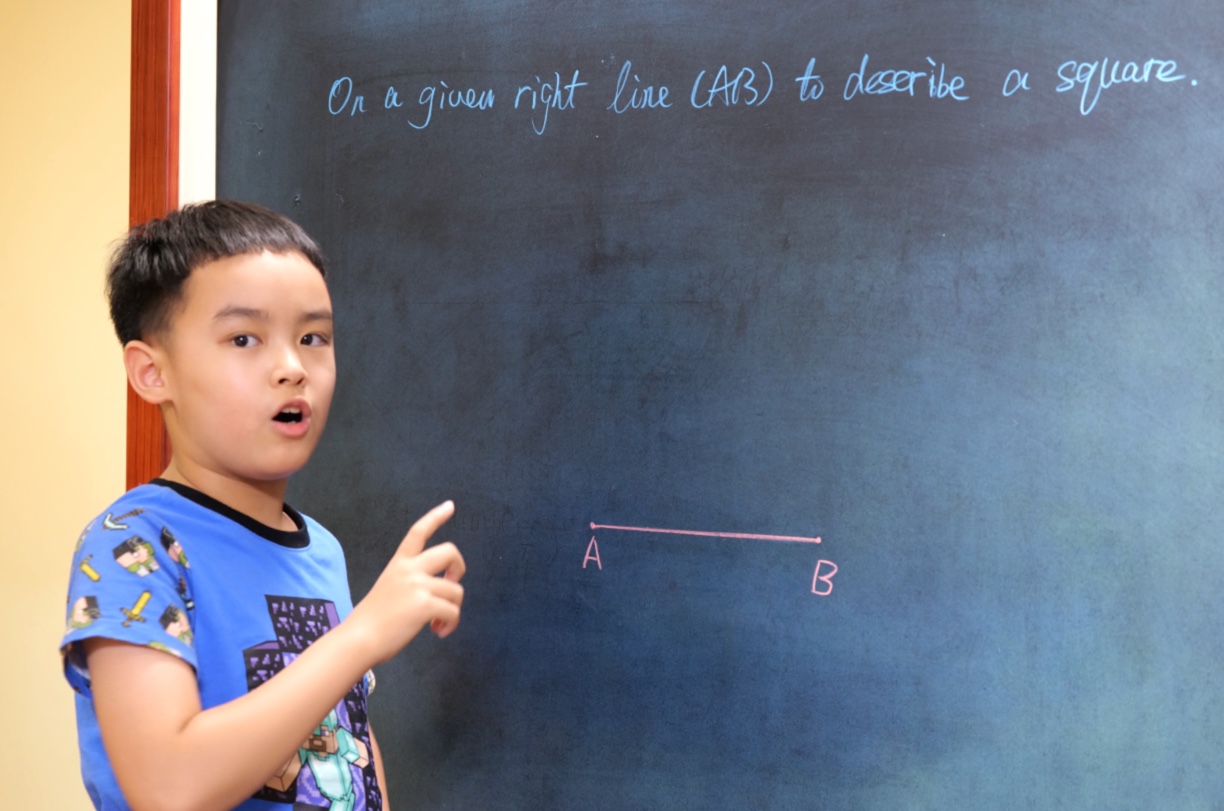
On a given right line (AB) to describe a square.
I am a student, learn, happy.
Always happy.