Mr. Eric
Life writes the best stories. Let’s study together! Never copy please!
© 2020 - 2023 Mr. Eric
© 2020 - 2023 Mr. Eric

Parallelograms on the same base (BC) and between the same parallels are equal.
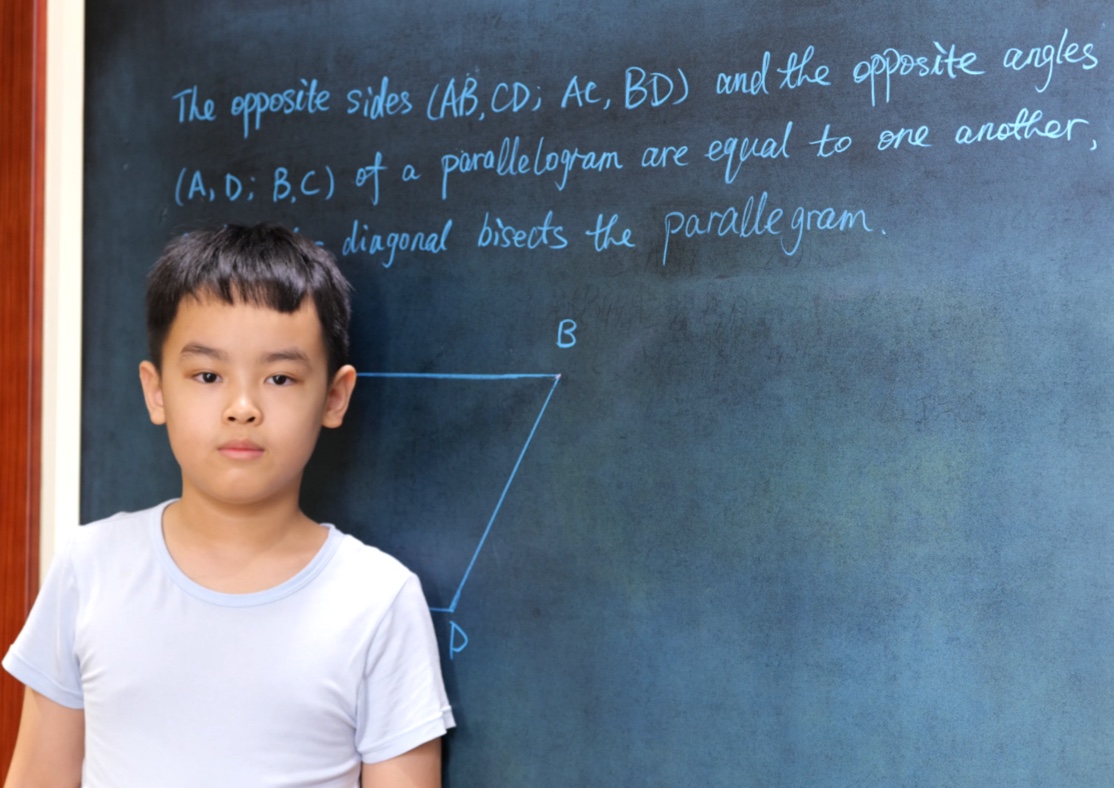
The opposite sides (AB, CD,; AC, BD) and the opposite angles (A, D; B, C) of a parallelogram are equal to one another, and either diagonal bisects the parallelogram.

The right lines (AC, BD) which join the adjacent extremities of two equal and parallel right lines (AB, CD) are equal and parallel.

If any side (AB) of a triangle (ABC) be produced (to D), the external angle (CBD) is equal to the sum of the two internal non-adjacent angles (A, C), and the sum of the three internal angles is equal to two right angles.

Through a given point (C) to draw a right line parallel to a given right line.

If two right lines (AB, CD) be parallel to the same right line (EF), they are parallel to one another.
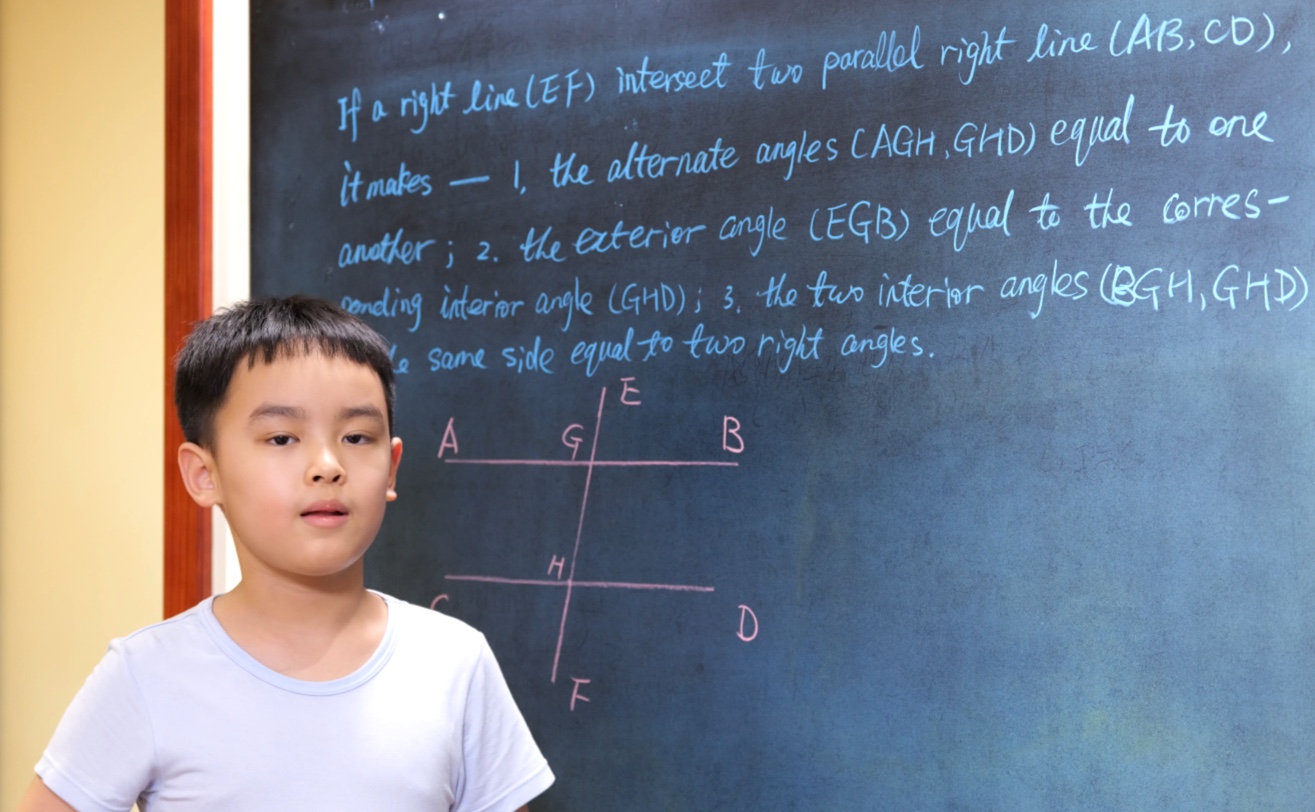
If a right line (EF) intersect two parallel right lines (AB, CD), it makes:

If a right line (EF) intersect two parallel right lines (AB, CD) makes the exterior angle (EGB) equal to its corresponding interior angle (GHD), or makes two interior angles (BGH, GHD) on the same side equal to two right angles, the two right lines are parallel.
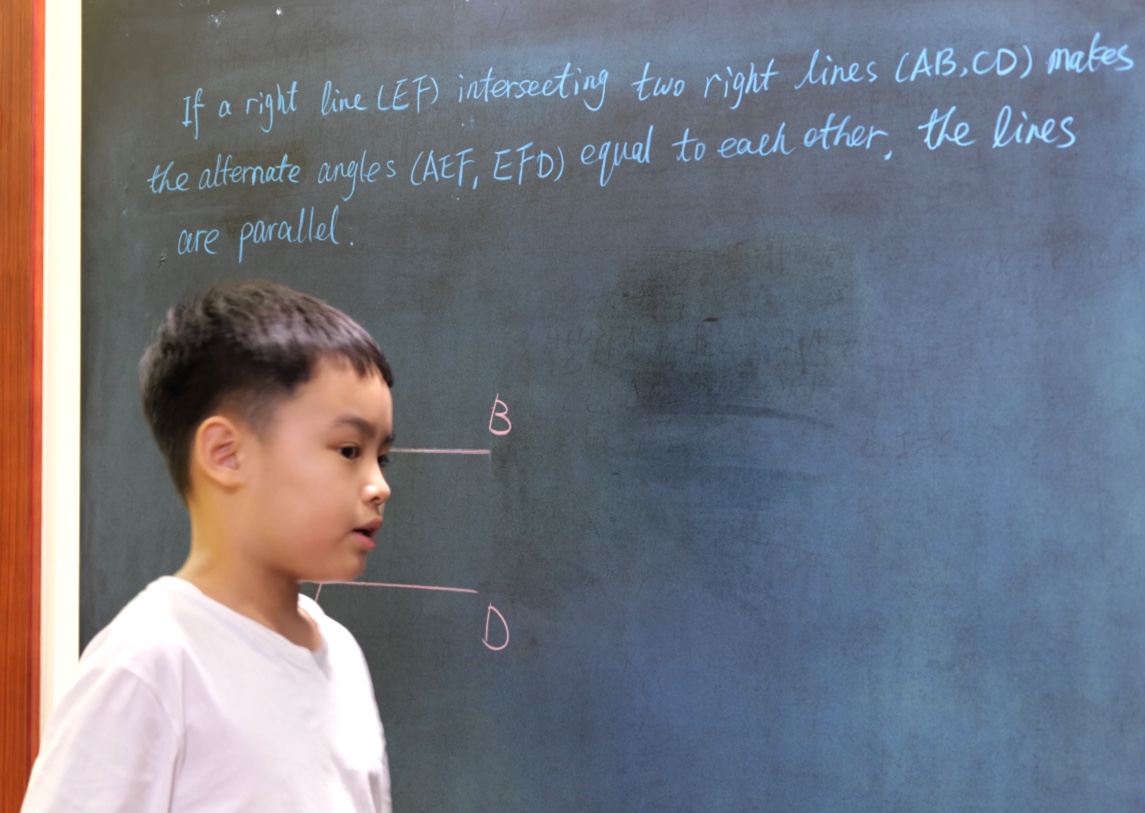
If a right line (EF) intersecting two right lines (AB, CD) makes the alternate angles (AEF, EFD) equal to each other, these lines are parallel.

If two triangles (ABC, DEF) have two angles B, C) of one equal respectively to two angles (E, F) of the other, and a side of one equal to a side similarly placed with respect to the equal angles of the other, the triangles are equal in every respect.
I am a student, learn, happy.
Always happy.