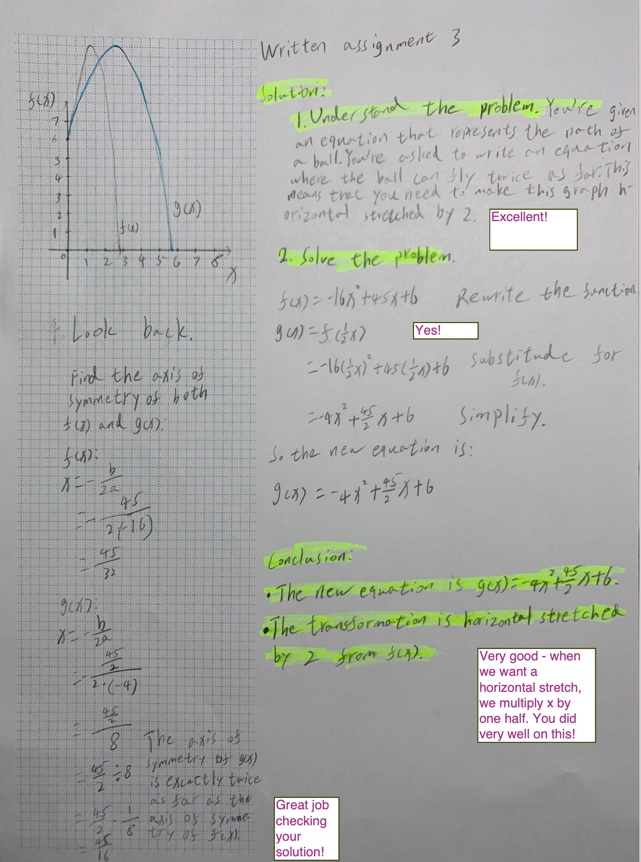
Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.
In this chapter we learned about functions in the form $g(x)=a(x-h)^2+k$.
- In your own words, how do the constants $a$, $h$, and $k$ affect the graph of $g(x)$? Clearly and completely explain the impact of each constant and provide examples with reasoning.
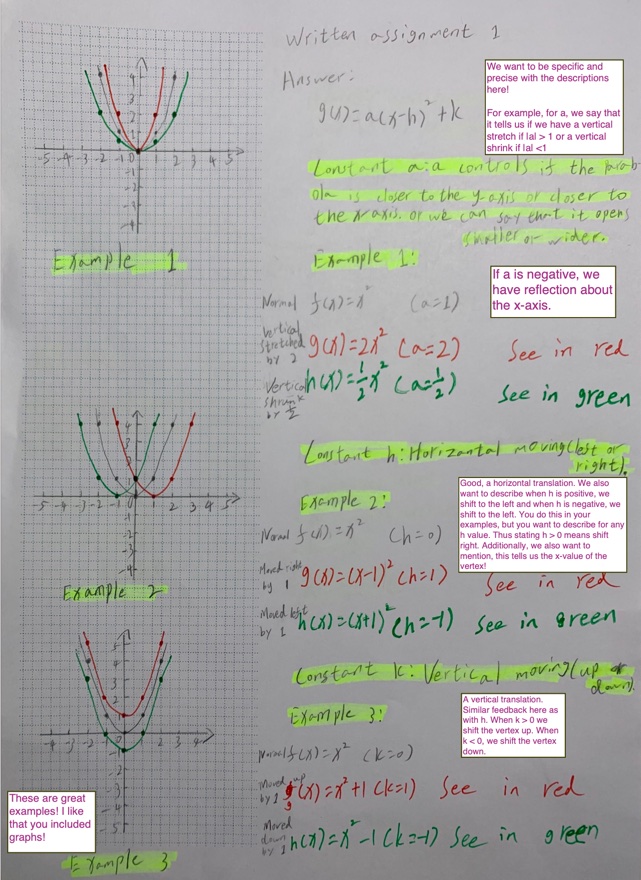
- Standard form of a quadratic equation is given as $y=ax^2+bx+c$ and vertex form is given as $y=a(x-h)^2+k$. Write a formula that relates the values of $a$, $b$, and $c$ in $y=ax^2+bx+c$ to the values of $a$, $h$, and $k$, in $y=a(x-h)^2+k$. For instance $h=ax+b$ would be a formula that relates $h$ to $a$ and $b$.

- The path of a ball thrown can be modeled by the equation $f(x)=-16x^2+45x+6$, where $x$ is the horizontal distance. Use a transformation to create a new model in which the ball is thrown twice as far. What is the new equation, what is the transformation, and how did you pick this? Remember, no graphing devices or calculators should be used.