Algebra Problem No.6

Think and Love

@ Mr. Eric | Tuesday, Aug 10, 2021 | 1 minute read | Update at Tuesday, Aug 10, 2021

Complete each problem below by hand. Show your work and provide a reason for each step. Calculators are not allowed on this assignment.

  1. Write a proof for the change of base formula. Remember, outside resources are not permitted and this should be 100% your own work. This formula can be proven using what you have learned in this course.

Answer

  1. Solve each of the following equations for $x$. Give specific reasoning for each step (not just listing a rule) and clearly conclude your solution.

a. $e^{ln(x^2-3)} = 2x$

Answer

b. $e^{2x}-e^x-12 = 0$

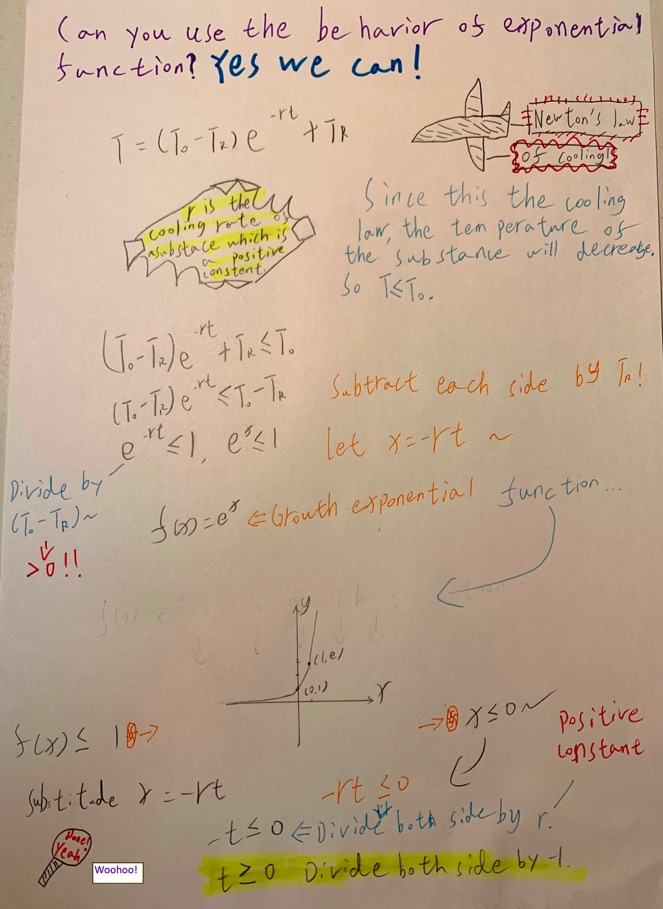
Answer

  1. A student has solved Newton’s Law of Cooling for time, $t$, and concludes the formula does not make sense as time is a negative value. Help the student to understand the formula. For simplicity, assume that $T_0 \gt T_R$ and $T \geq T_R$.

a. Solve Newton’s Law of Cooling $T = (T_0-T_R)e^{-rt}+T_R$ where $T_0$ is the initial temperature, $T$ is the temerature after $t$ minutes, and $T_R$ is the room temperature for time $t$.

Answer

b. Consider the value of $\dfrac{T-T_R}{T_0-T_R}$ and determine what are the possible values for this rational expression.

Answer

c. Explain to the student using the behavior of exponential/logarithmic functions why $t \geq 0$.

Answer

Answer

Mr. Eric
Life writes the best stories. Let’s study together! Never copy please!
A Friendly Introduction to Number Theory Algebra Ii Algebra Problem Algorithm Code Euclid Geometry Germination Method Number Theory Opinion Poetry Appreciation Reflection Seed Solve Speech Stop Motion
Algebra
Algebra Problem No.11
Algebra Problem No.9
Algebra Problem No.8
Algebra Problem No.7
Algebra Problem No.6
Algebra Problem No.5
Algebra Problem No.4
Algebra Problem No.3
Algebra Problem No.2
Algebra Problem No.1
Free Question No.1
Algorithm
Algorithms Code Quick Sort
Algorithms Chapter 2
Algorithms Chapter 1
Code
Algorithms Code Quick Sort
Essay
Dehumanization of slaves
‘A Long Walk To Water’ Reading Reflection (G5)
Biography about Nikola Tesla (G4)
Oh the places you'll go!
Ways To Express Yourself (G4)
Volunteer or not (G4)
Should We Reach Out (G4)
Geometry
Euclid Book II PROP. XIII. -- THEROREM.
Euclid Book II PROP. XII. -- THEROREM.
Euclid Book II PROP. XI. -- PROBLEM.
Euclid Book II PROP. X. -- THEOREM.
Euclid Book II PROP. IX. -- THEOREM.
Euclid Book II PROP. VIII. -- THEOREM.
Euclid Book II PROP. VII. -- THEOREM.
Euclid Book II PROP. VI. -- THEOREM.
Euclid Book II PROP. V. -- THEOREM.
Euclid Book II PROP. IV. -- THEOREM.
Euclid Book II PROP. III. -- THEOREM.
Euclid Book II PROP. II. -- THEOREM.
Euclid Book II PROP. I. -- THEOREM.
Euclid Book I PROP. XLVIII. -- THEOREM.
Euclid Book I PROP. XLVII. -- THEOREM.
Euclid Book I PROP. XLVI. -- PROBLEM.
Euclid Book I PROP. XLV. -- PROBLEM.
Euclid Book I PROP. XLIV. -- PROBLEM.
Euclid Book I PROP. XLIII. -- THEOREM.
Euclid Book I PROP. XLII. -- PROBLEM.
Euclid Book I PROP. XLI. -- THEOREM.
Euclid Book I PROP. XL. -- THEOREM.
Euclid Book I PROP. XXXIX. -- THEOREM.
Euclid Book I PROP. XXXVIII. -- THEOREM.
Euclid Book I PROP. XXXVII. -- THEOREM.
Euclid Book I PROP. XXXVI. -- THEOREM.
Euclid Book I PROP. XXXV. -- THEOREM.
Euclid Book I PROP. XXXIV. -- THEOREM.
Euclid Book I PROP. XXXIII. -- THEOREM.
Euclid Book I PROP. XXXII. -- THEOREM.
Euclid Book I PROP. XXXI. -- PROBLEM.
Euclid Book I PROP. XXX. -- THEOREM.
Euclid Book I PROP. XXIX. -- THEOREM.
Euclid Book I PROP. XXVIII. -- THEOREM.
Euclid Book I PROP. XXVII. -- THEOREM.
Euclid Book I PROP. XXVI. -- THEOREM.
Euclid Book I PROP. XXV. -- THEOREM.
Euclid Book I PROP. XXIV. -- THEOREM.
Euclid Book I PROP. XXIII. -- PROBLEM.
Euclid Book I PROP. XXII. -- PROBLEM.
Euclid Book I PROP. XXI. -- THEOREM.
Euclid Book I PROP. XX. -- THEOREM.
Euclid Book I PROP. XIX. -- THEOREM.
Euclid Book I PROP. XVIII. -- THEOREM.
Euclid Book I PROP. XVII. -- THEOREM.
Euclid Book I PROP. XVI. -- THEOREM.
Euclid Book I PROP. XV. -- THEOREM.
Euclid Book I PROP. XIV. -- THEOREM.
Euclid Book I PROP. XIII. -- THEOREM.
Euclid Book I PROP. XII. -- PROBLEM.
Euclid Book I PROP. XI. -- PROBLEM.
Euclid Book I PROP. X. -- PROBLEM.
Euclid Book I PROP. IX. -- PROBLEM.
Euclid Book I PROP. VIII. -- THEOREM.
Euclid Book I PROP. VII. -- THEOREM.
Euclid Book I PROP. VI. – THEOREM.
Euclid Book I PROP. V. – THEOREM.
Euclid Book I PROP. IV. – THEOREM.
Euclid Book I PROP. III. – PROBLEM.
Euclid Book I PROP. II. – PROBLEM.
Euclid Book I PROP. I. – PROBLEM.
Number Theory
What is number theory
......

© 2020 - 2023 Mr. Eric

Powered by Hugo with theme Dream.

Mr. Eric

I am a student, learn, happy.

Always happy.