Algebra Problem No.7

Think and Love

@ Mr. Eric | Monday, Aug 16, 2021 | 1 minute read | Update at Monday, Aug 16, 2021

Complete each problem below by hand. Show your work and provide a reason for each step. Calculators or other graphing devices are not allowed on this assignment.

  1. Simplify the following complex fraction to linear factors.

$$ \dfrac{\frac{6}{x^2+2x-15}-\frac{1}{x-3}}{\frac{1}{x+5}+1} $$

What are the key points of this function? When is this function positive?

Answer

Oops … missing question “When is this function positive”

Answer

  1. Solve the rational inquality

$$ \dfrac{x^2-3x-2}{x^2+5x+6}>\dfrac{2-x}{x^2-4} $$

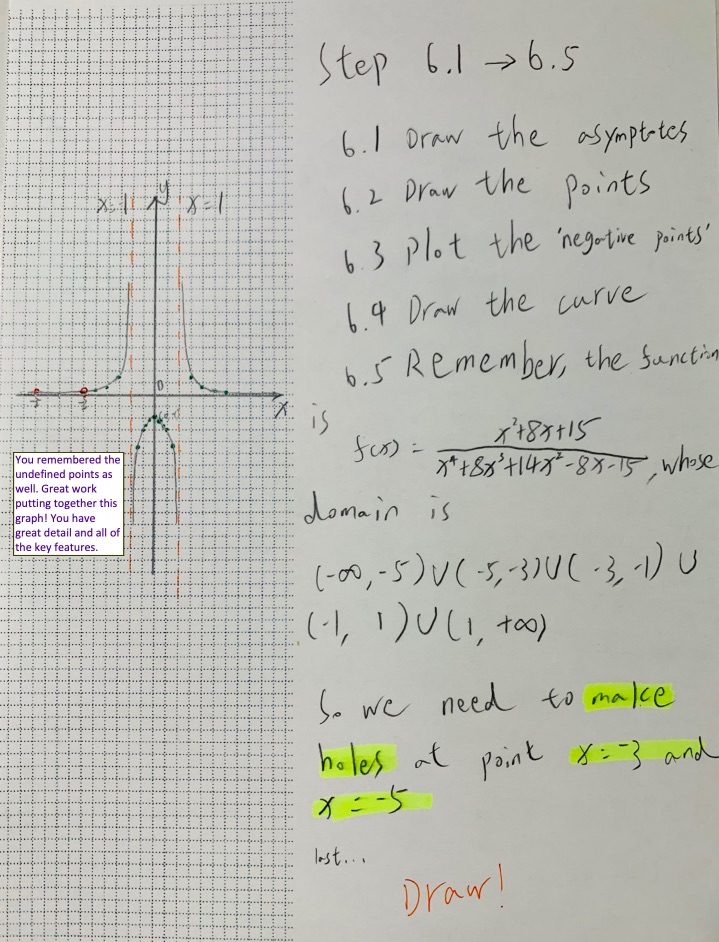
Answer

  1. Consider the rational function

$$ f(x)=\dfrac{x^2+8x+15}{x^4+8x^3+14x^2-8x-15} $$

Notice the denominator is the same as your work on Algebra Problem: Chapter 4. Use your previous results to:

a. Find all zeros of $f(x)$.

Answer

b. Find the asymptotes.

Answer

c. Sketch a graph $f(x)$ including all key features previously found. Include how you graphed.

Answer

Answer

Answer

Mr. Eric
Life writes the best stories. Let’s study together! Never copy please!
A Friendly Introduction to Number Theory Algebra Ii Algebra Problem Algorithm Code Euclid Geometry Germination Method Number Theory Opinion Poetry Appreciation Reflection Seed Solve Speech Stop Motion
Algebra
Algebra Problem No.11
Algebra Problem No.9
Algebra Problem No.8
Algebra Problem No.7
Algebra Problem No.6
Algebra Problem No.5
Algebra Problem No.4
Algebra Problem No.3
Algebra Problem No.2
Algebra Problem No.1
Free Question No.1
Algorithm
Algorithms Code Quick Sort
Algorithms Chapter 2
Algorithms Chapter 1
Code
Algorithms Code Quick Sort
Essay
Dehumanization of slaves
‘A Long Walk To Water’ Reading Reflection (G5)
Biography about Nikola Tesla (G4)
Oh the places you'll go!
Ways To Express Yourself (G4)
Volunteer or not (G4)
Should We Reach Out (G4)
Geometry
Euclid Book II PROP. XIII. -- THEROREM.
Euclid Book II PROP. XII. -- THEROREM.
Euclid Book II PROP. XI. -- PROBLEM.
Euclid Book II PROP. X. -- THEOREM.
Euclid Book II PROP. IX. -- THEOREM.
Euclid Book II PROP. VIII. -- THEOREM.
Euclid Book II PROP. VII. -- THEOREM.
Euclid Book II PROP. VI. -- THEOREM.
Euclid Book II PROP. V. -- THEOREM.
Euclid Book II PROP. IV. -- THEOREM.
Euclid Book II PROP. III. -- THEOREM.
Euclid Book II PROP. II. -- THEOREM.
Euclid Book II PROP. I. -- THEOREM.
Euclid Book I PROP. XLVIII. -- THEOREM.
Euclid Book I PROP. XLVII. -- THEOREM.
Euclid Book I PROP. XLVI. -- PROBLEM.
Euclid Book I PROP. XLV. -- PROBLEM.
Euclid Book I PROP. XLIV. -- PROBLEM.
Euclid Book I PROP. XLIII. -- THEOREM.
Euclid Book I PROP. XLII. -- PROBLEM.
Euclid Book I PROP. XLI. -- THEOREM.
Euclid Book I PROP. XL. -- THEOREM.
Euclid Book I PROP. XXXIX. -- THEOREM.
Euclid Book I PROP. XXXVIII. -- THEOREM.
Euclid Book I PROP. XXXVII. -- THEOREM.
Euclid Book I PROP. XXXVI. -- THEOREM.
Euclid Book I PROP. XXXV. -- THEOREM.
Euclid Book I PROP. XXXIV. -- THEOREM.
Euclid Book I PROP. XXXIII. -- THEOREM.
Euclid Book I PROP. XXXII. -- THEOREM.
Euclid Book I PROP. XXXI. -- PROBLEM.
Euclid Book I PROP. XXX. -- THEOREM.
Euclid Book I PROP. XXIX. -- THEOREM.
Euclid Book I PROP. XXVIII. -- THEOREM.
Euclid Book I PROP. XXVII. -- THEOREM.
Euclid Book I PROP. XXVI. -- THEOREM.
Euclid Book I PROP. XXV. -- THEOREM.
Euclid Book I PROP. XXIV. -- THEOREM.
Euclid Book I PROP. XXIII. -- PROBLEM.
Euclid Book I PROP. XXII. -- PROBLEM.
Euclid Book I PROP. XXI. -- THEOREM.
Euclid Book I PROP. XX. -- THEOREM.
Euclid Book I PROP. XIX. -- THEOREM.
Euclid Book I PROP. XVIII. -- THEOREM.
Euclid Book I PROP. XVII. -- THEOREM.
Euclid Book I PROP. XVI. -- THEOREM.
Euclid Book I PROP. XV. -- THEOREM.
Euclid Book I PROP. XIV. -- THEOREM.
Euclid Book I PROP. XIII. -- THEOREM.
Euclid Book I PROP. XII. -- PROBLEM.
Euclid Book I PROP. XI. -- PROBLEM.
Euclid Book I PROP. X. -- PROBLEM.
Euclid Book I PROP. IX. -- PROBLEM.
Euclid Book I PROP. VIII. -- THEOREM.
Euclid Book I PROP. VII. -- THEOREM.
Euclid Book I PROP. VI. – THEOREM.
Euclid Book I PROP. V. – THEOREM.
Euclid Book I PROP. IV. – THEOREM.
Euclid Book I PROP. III. – PROBLEM.
Euclid Book I PROP. II. – PROBLEM.
Euclid Book I PROP. I. – PROBLEM.
Number Theory
What is number theory
......

© 2020 - 2023 Mr. Eric

Powered by Hugo with theme Dream.

Mr. Eric

I am a student, learn, happy.

Always happy.