a. Assume that the length and width of a rectangle can be only whole numbers. How many rectangles of different dimensions have a perimeter of 12? 14? 16? 18? 24? (Orientation of the rectangle does not matter; that is, a 2x3 is the same rectangle as a 3x2.)
b. How many rectangles of different whole-number dimensions have a perimeter of n? Write your answer as an expression in n and explain your reasoning.
c. Assume that the length and width of a rectangle can be only whole numbers. Could the perimeter, n, be an odd-number? Explain why or why not.
Answer for question A:
$$ 12(3) \qquad 14(3) \qquad 16(4) \qquad 18(4) \qquad 24(6) $$
Strategy:
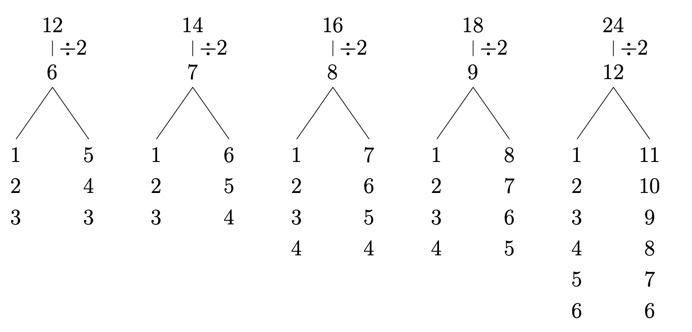
Answer for question B:
Firstly, divide the perimeter, n by two. Then, if you get an even number, divide it by two again and that’s the answer! And if you get an odd number, minus one first the divide by two. The answer. We divide n by two because a rectangle’s perimeter is (width + length) × 2. So if we divide two, we got the sum of width and length. The next step is…You can see from the picture above. It’s just experience.
Answer for question C:
Probably NO!! Because if n is an odd number, the sum of width and length will have a decimal part! Then at least one of width or length must have a decimal part, which is Prohibit! It’s outside the rule!