© 2020 - 2023 Mr. Eric

Euclid Book II PROP. XIII. -- THEROREM.
In any triangle (ABC), the square on any side subtending an acute angle (C) is less than the sum of the squares on the sides containing that angle, by twice the rectangle (BC, CD) contained by either of them (BC) and the intercept (CD) between the acute angle and the foot of the perpendicular on it from the opposite angle.
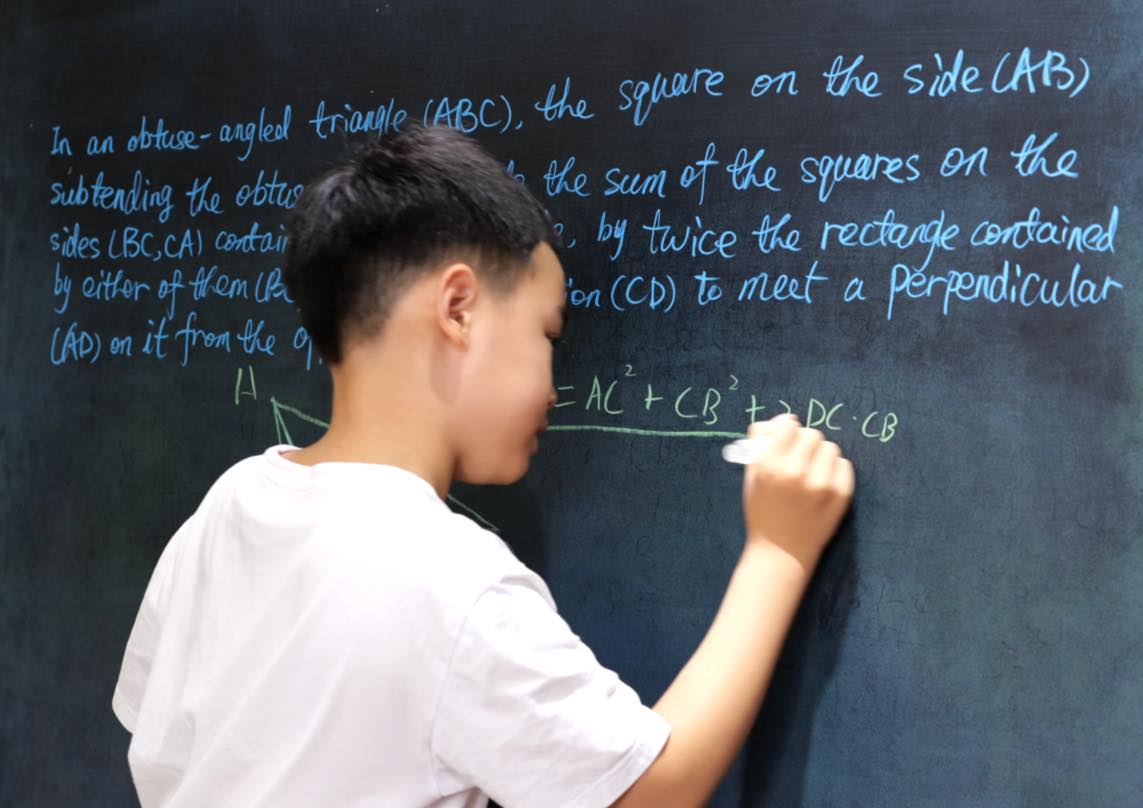
Euclid Book II PROP. XII. -- THEROREM.
In an obtuse-angled triangle (ABC), the square on the side (AB) subtending the obtuse angle exceeds the sum of squares on the sides (BC, CA) containing the obtuse angle, by twice the rectangle contained by either of them (BC), and its continuation (CD) to meet a perpendicular (AD) on it from the opposite angle.
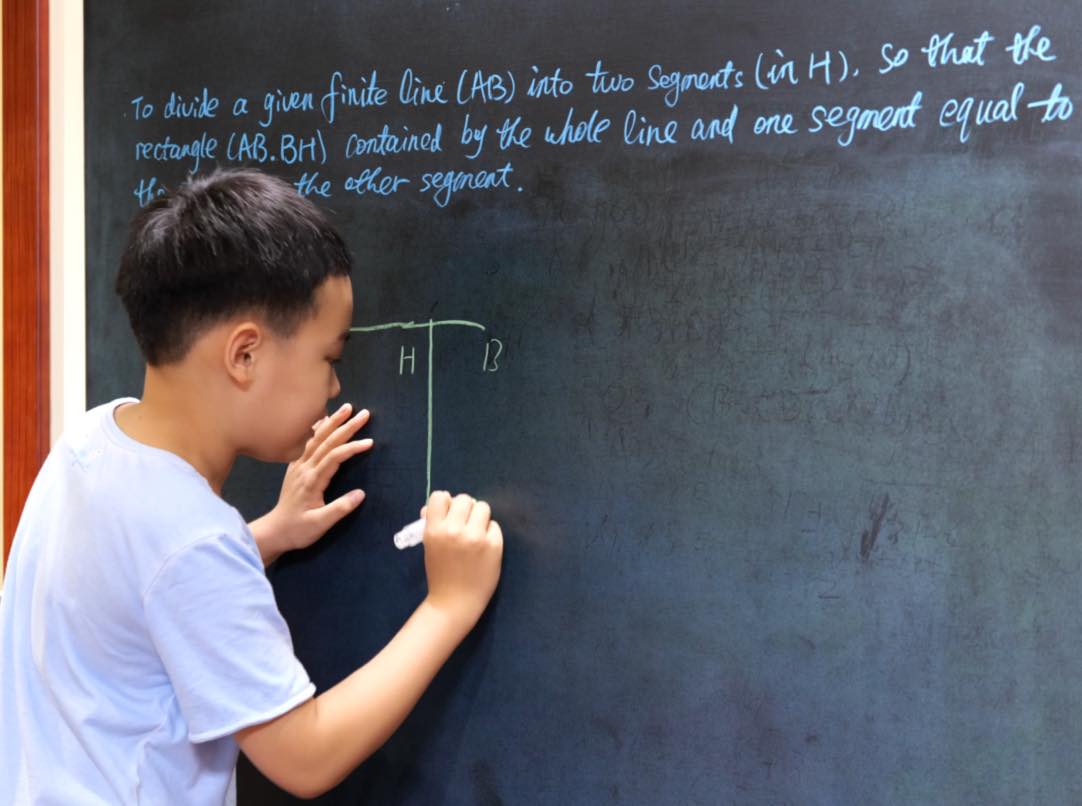
Euclid Book II PROP. XI. -- PROBLEM.
To divide a given finite line (AB) into two segments (in H), so that the rectangle (AB. BH) contained by the whole line and one segment may be equal to the square on the other segment.
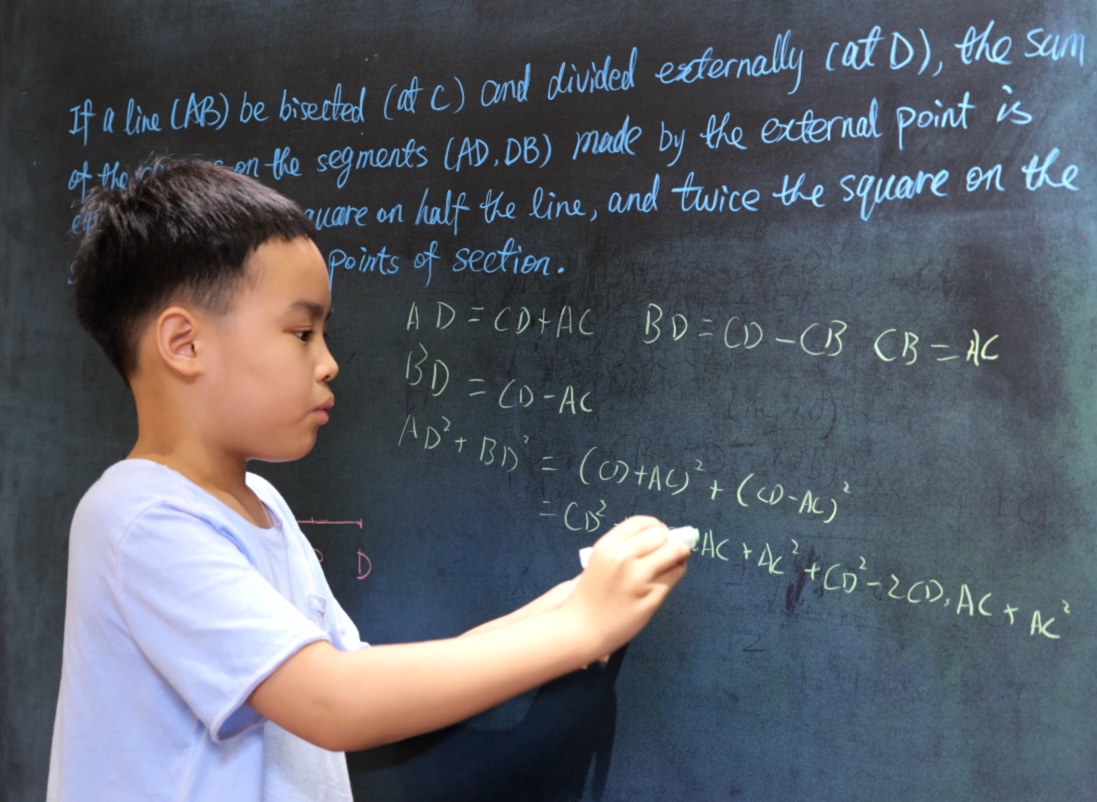
Euclid Book II PROP. X. -- THEOREM.
If a line (AB) be bisected (at C) and divided externally (at D), the sum of the squares on the segments (AD, DB) made by the external point is equal to twice the square on half the line, and twice the square on the segment between the points of section.

Euclid Book II PROP. IX. -- THEOREM.
If a line (AB) be bisected (at C) and divided into two unequal parts (at D), the sum of the squares on the unequal parts (AD, DB) is double the sum of the squares on half the line (AC), and on the segment (CD) between the points of section.
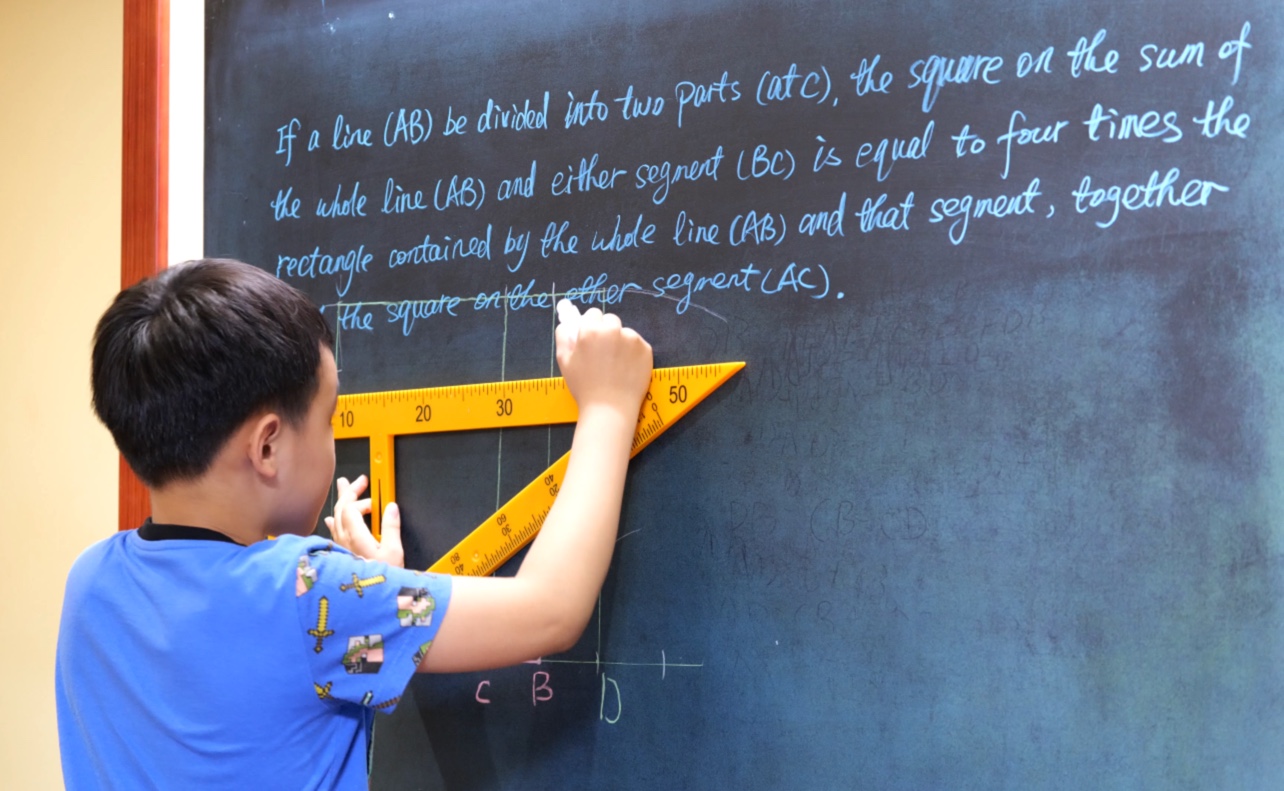
Euclid Book II PROP. VIII. -- THEOREM.
If a line (AB) be divided into two parts (at C), the square on the sum the whole line (AB) and either segment (BC) is equal to four times the rectangle contained by the whole line (AB) and that segment, together with the square on the other segment (AC).
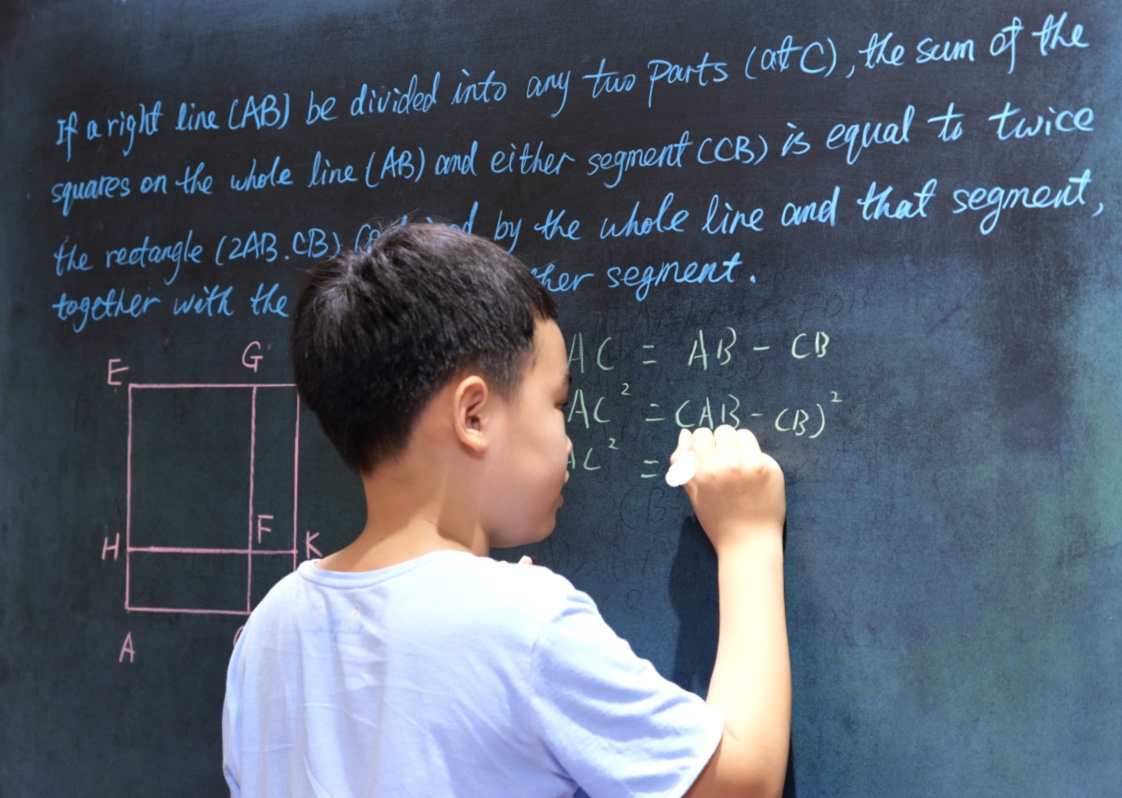
Euclid Book II PROP. VII. -- THEOREM.
If a right line (AB) be divided into any two parts (at C), the sum of the squares on the whole line (AB) and either segment (CB) is equal to twice the rectangle (2AB.CB) contained by the whole line and that segment, together with the square on the other segment.

Euclid Book II PROP. VI. -- THEOREM.
If a line (AB) be bisected (at C), and divided externally in any point (D), the rectangle (AD.BD) contained by the segments made by the external point, together with the square on half the line, is equal to the square on the segment between the middle point and the point of external division.
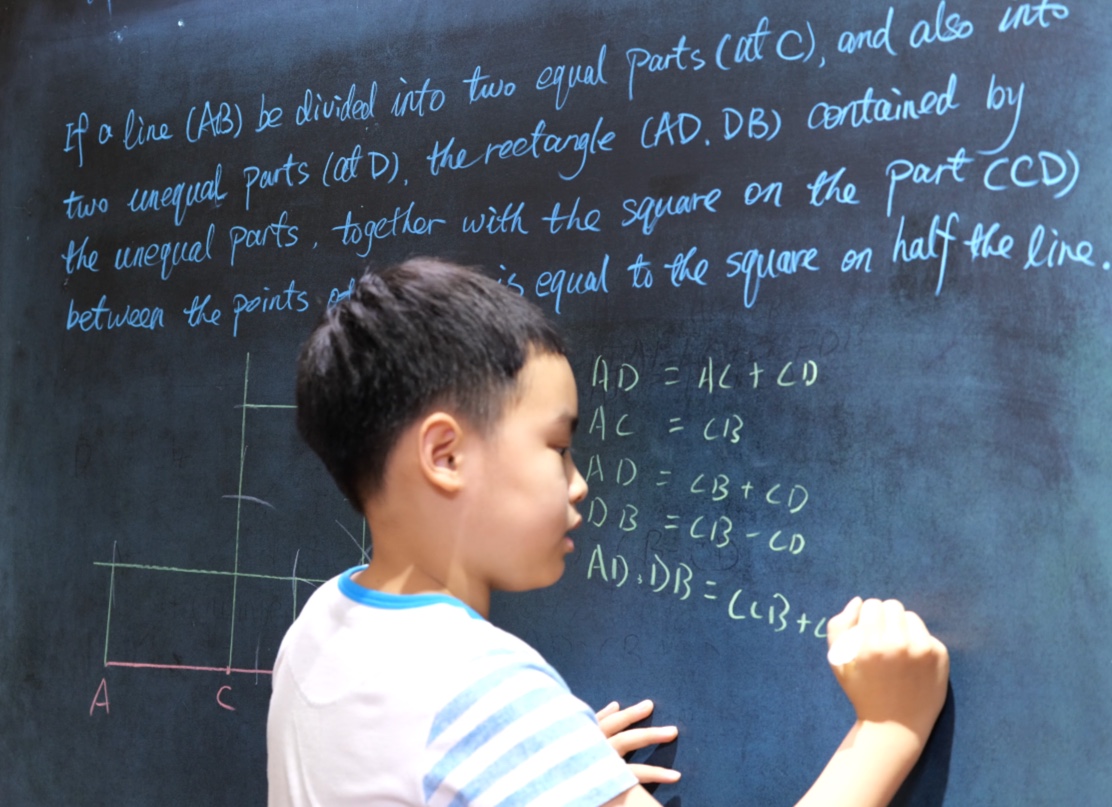
Euclid Book II PROP. V. -- THEOREM.
If a line (AB) be divided into two equal parts (at C), and also into two unequal parts (at D), the rectangle (AD.DB) contained by the unequal parts, together with the square on the part (CD) between the points of section, is equal to the square on half the line.

Euclid Book II PROP. IV. -- THEOREM.
If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the squares on the parts (AC, CB), together with twice their rectangle.
Mr. Eric
I am a student, learn, happy.
Always happy.