© 2020 - 2023 Mr. Eric
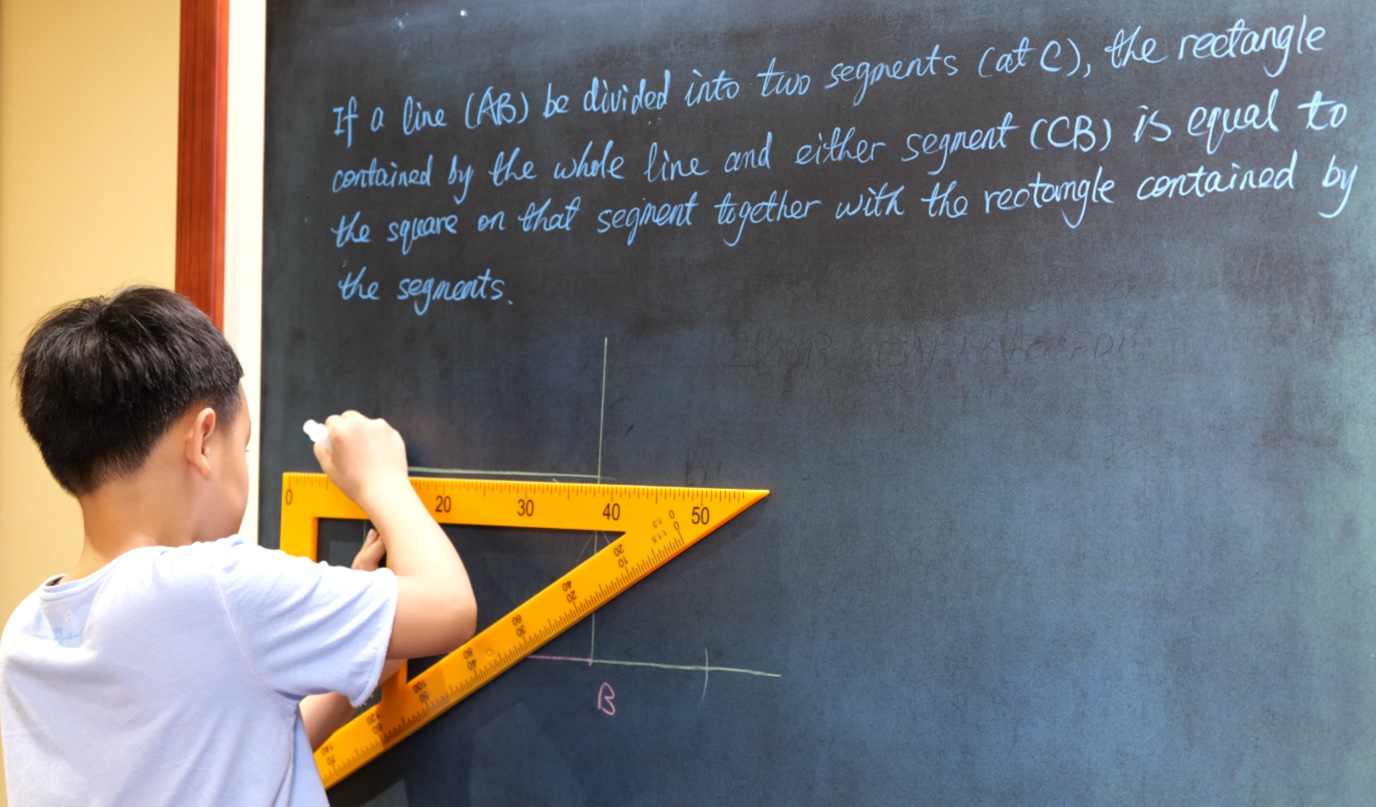
Euclid Book II PROP. III. -- THEOREM.
If a line (AB) be divided into two segments (at C), the rectangle contained by the whole line and either segment (CB) is equal to the square on that segment together with the rectangle contained by the segments.
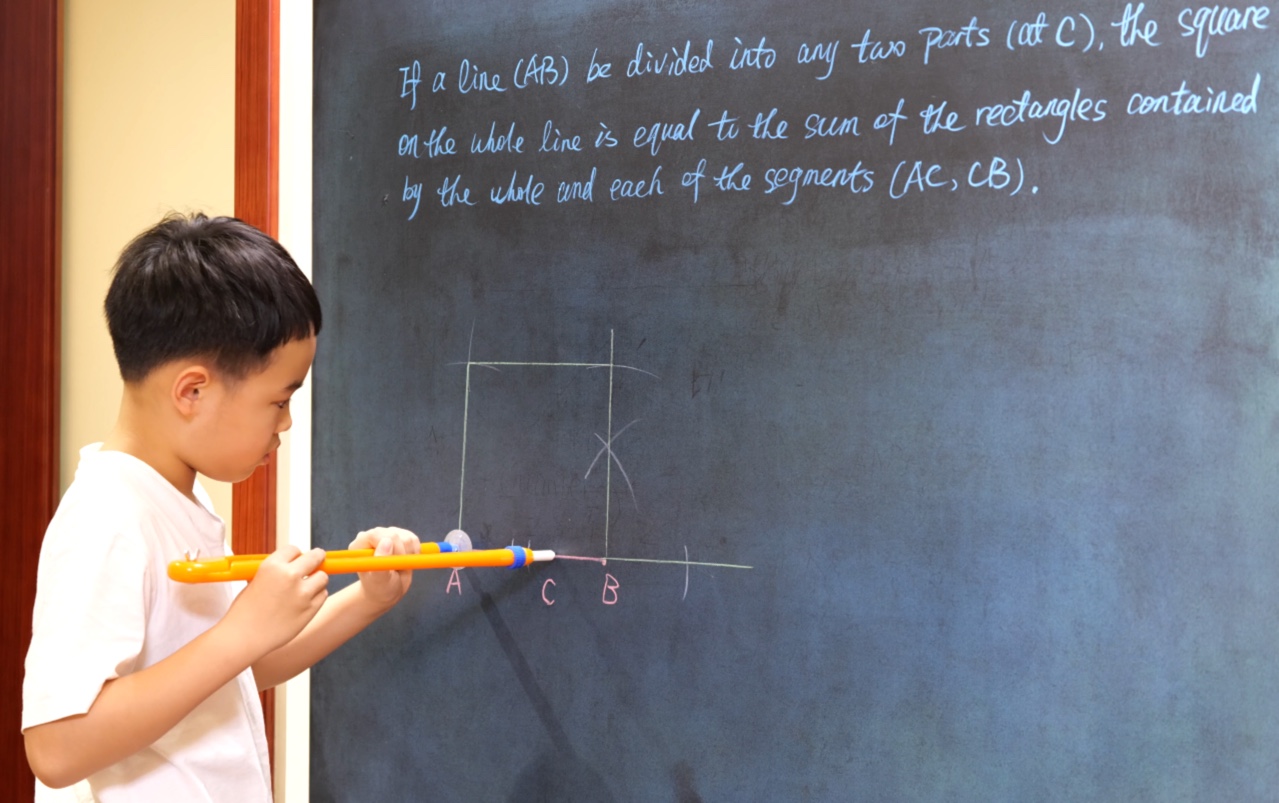
Euclid Book II PROP. II. -- THEOREM.
If a line (AB) be divided into any two parts (at C), the square on the whole line is equal to the sum of the rectangles contained by the whole and each of the segments (AC, CB).
Euclid Book II PROP. I. -- THEOREM.
If there be two lines (A, BC), one of which is divided into any number of parts (BD, DE, EC), the rectangle contained by the two lines (A, BC), is equal to the sum of the rectangles contained by the undivided line (A) and the several parts of the divided line.
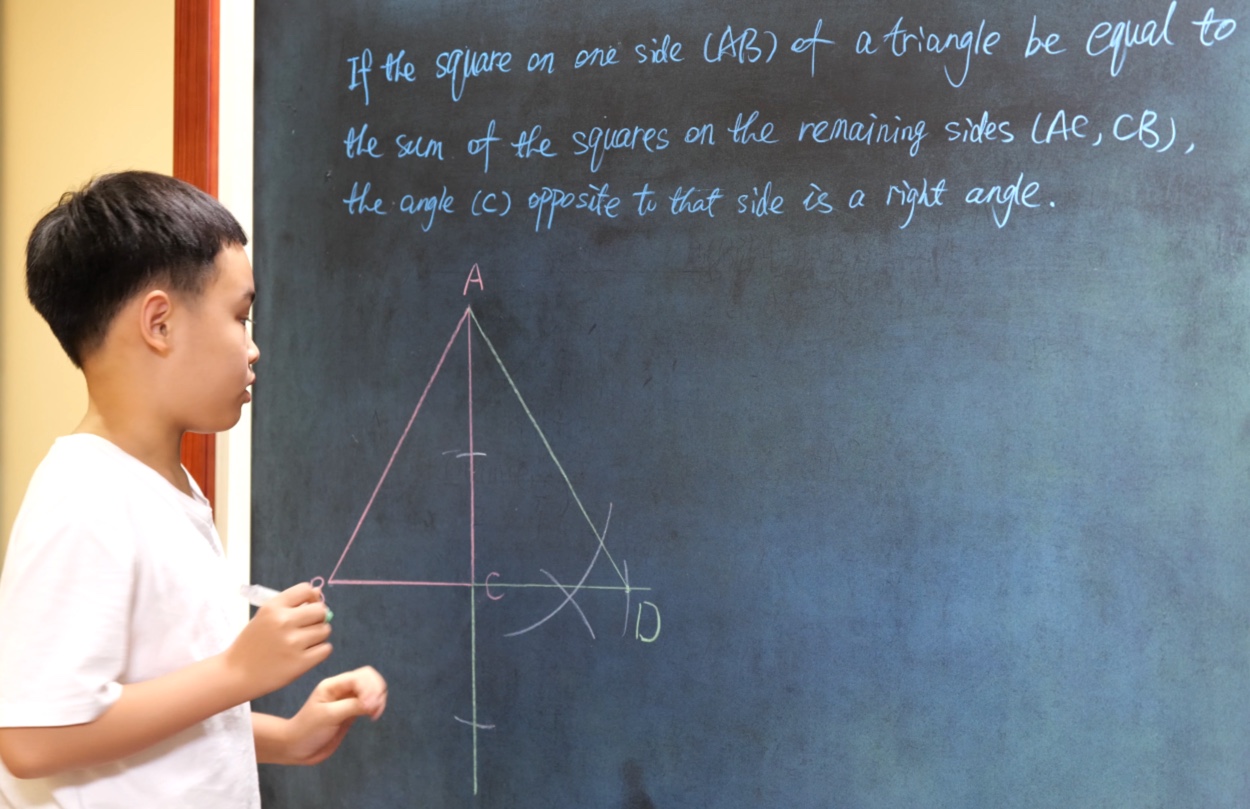
Euclid Book I PROP. XLVIII. -- THEOREM.
If the square on one side (AB) of a triangle be equal to the sum of the squares on the remaining sides (AC, CB), the angle (C) opposite to that side is a right angle.

Euclid Book I PROP. XLVII. -- THEOREM.
In a right-angled triangle (ABC) the square on the hypotenuse (AB) is equal to the sum of the squares on the other two sides (AC, BC).
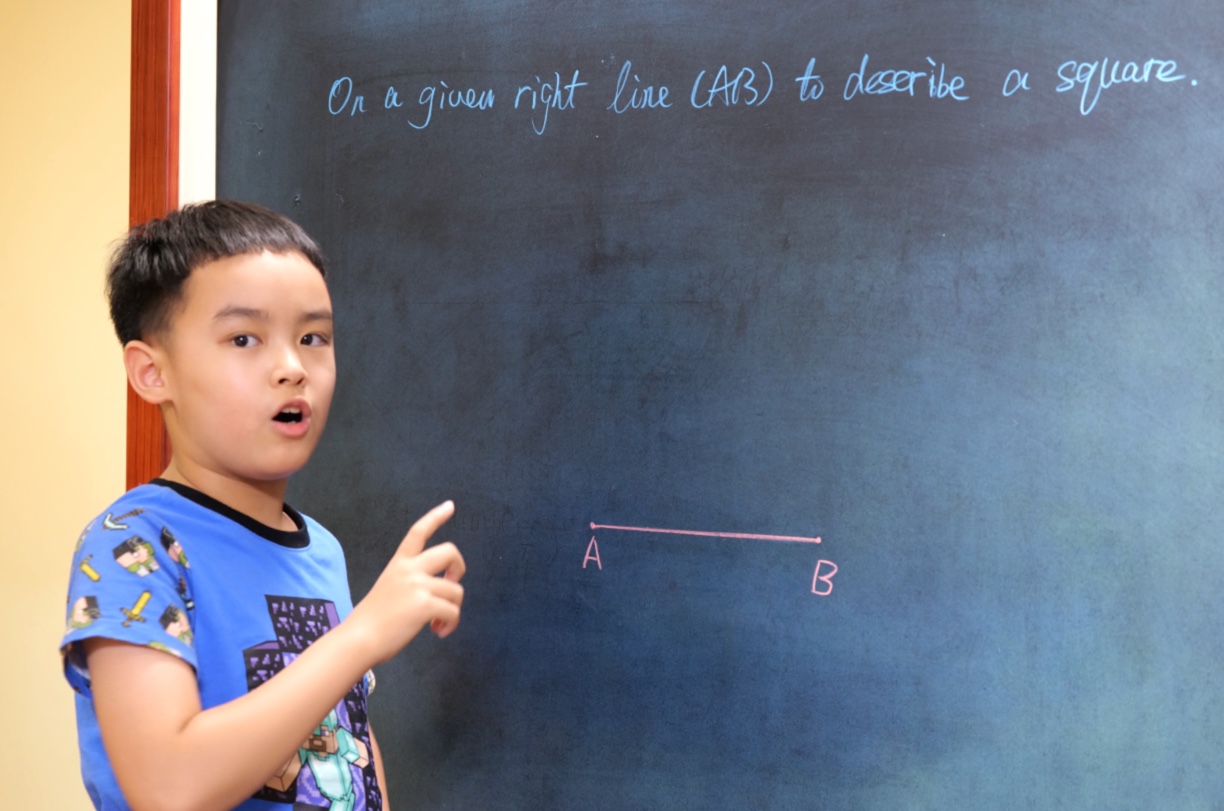
Euclid Book I PROP. XLVI. -- PROBLEM.
On a given right line (AB) to describe a square.
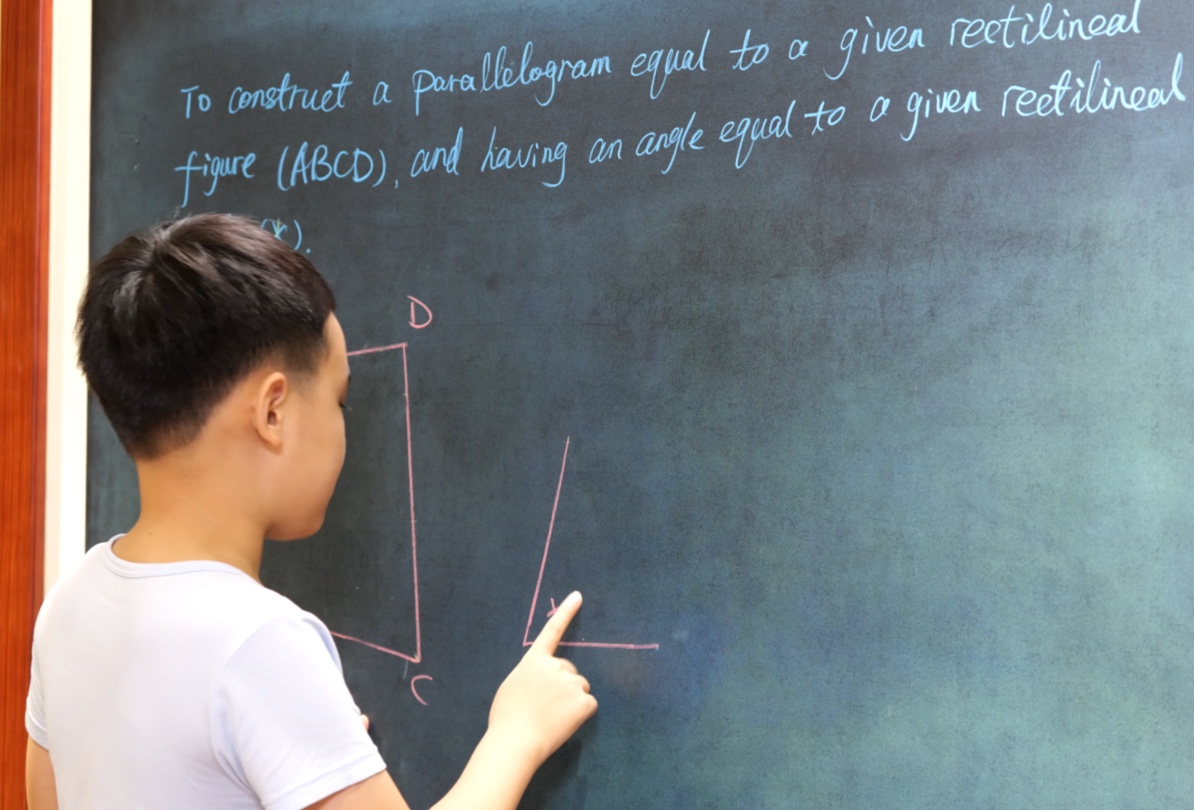
Euclid Book I PROP. XLV. -- PROBLEM.
To construct a parallelogram equal to a given rectilineal figure (ABCD), and having an angle equal to a given rectilineal angle (X).
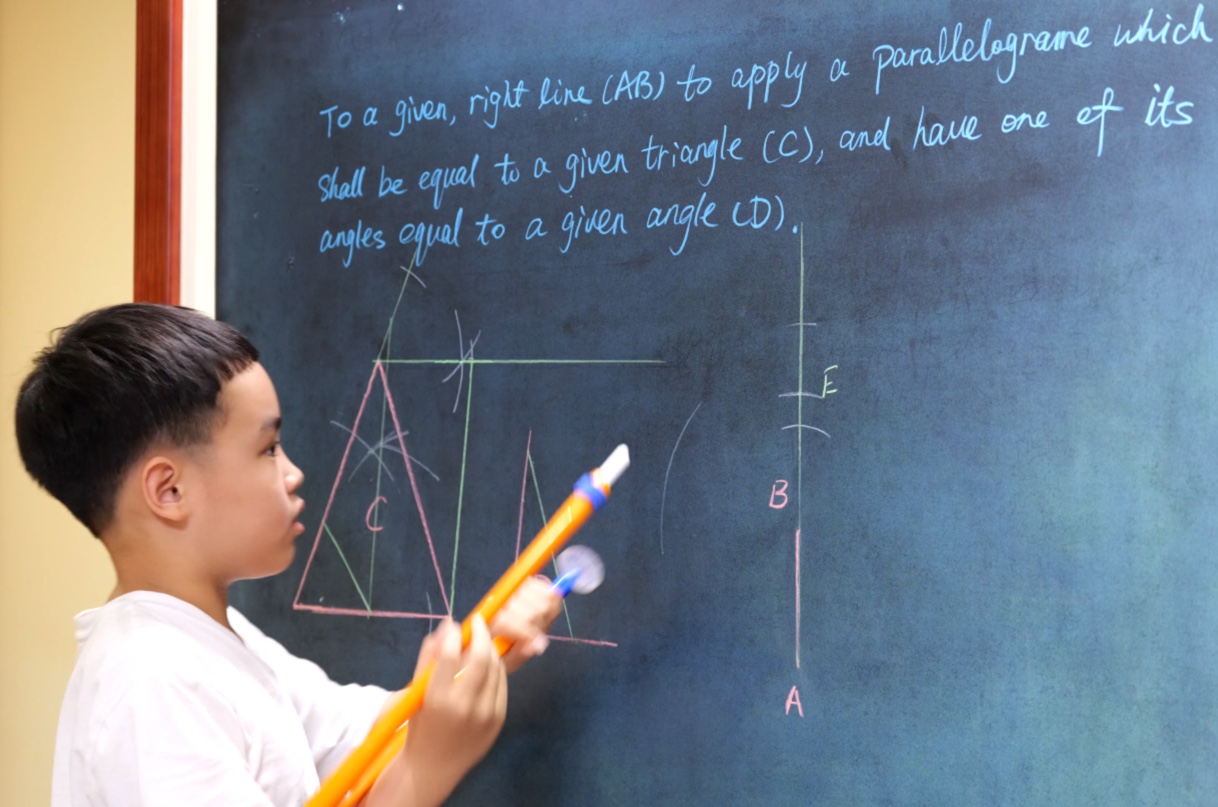
Euclid Book I PROP. XLIV. -- PROBLEM.
To a given, right line (AB) to apply a parallelogram which shall be equal to a given triangle (C), and have one of its angles equal to a given angle (D).

Euclid Book I PROP. XLIII. -- THEOREM.
In any parallelogram the complements of the parallelograms about the diameter equal one another.
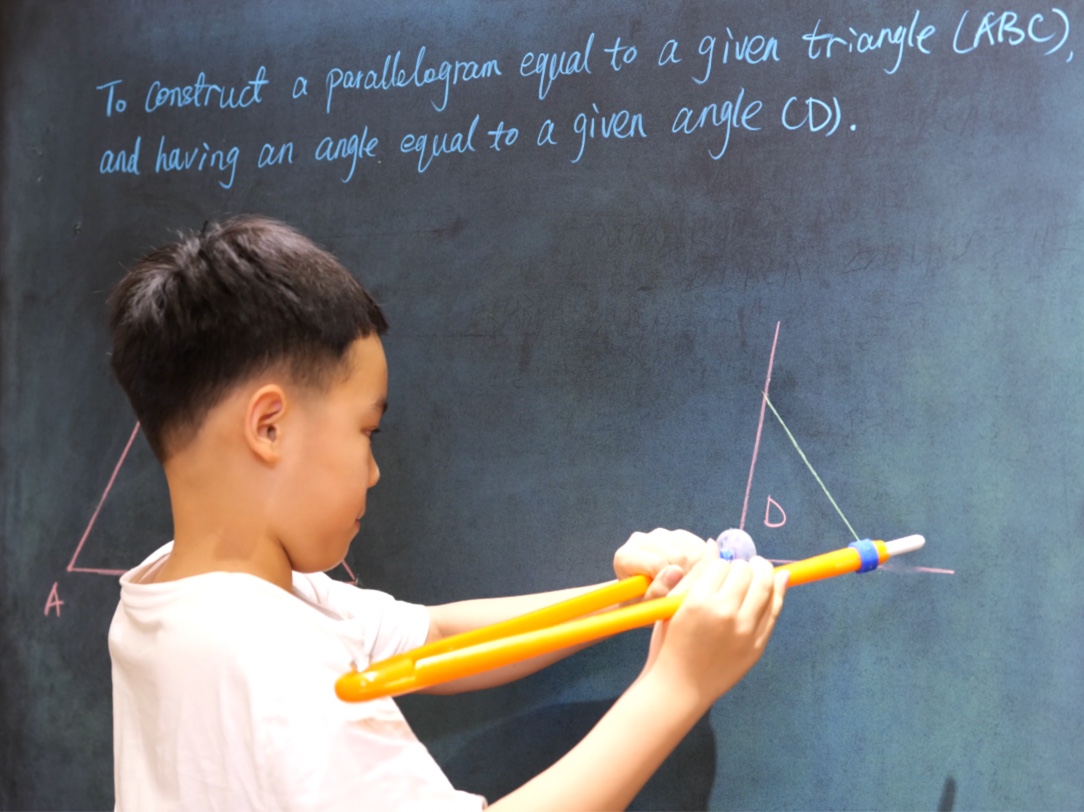
Euclid Book I PROP. XLII. -- PROBLEM.
To construct a parallelogram equal to a given triangle (ABC), and having an angle equal to a given angle (D).
Mr. Eric
I am a student, learn, happy.
Always happy.